
如圖所示,已知A( ,y1),B(2,y2)為反比例函數y=
,y1),B(2,y2)為反比例函數y= 圖象上的兩點,動點P(x,0)在x軸正半軸上運動,當線段AP與線段BP之差達到最大時,點P的坐標是( )
圖象上的兩點,動點P(x,0)在x軸正半軸上運動,當線段AP與線段BP之差達到最大時,點P的坐標是( )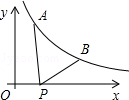
A.(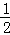 ,0) ,0) | B.(1,0) | C.(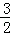 ,0) ,0) | D.( ,0) ,0) |
D
解析試題分析:求出AB的坐標,設直線AB的解析式是y=kx+b,把A、B的坐標代入求出直線AB的解析式,根據三角形的三邊關系定理得出在△ABP中,|AP﹣BP|<AB,延長AB交x軸于P′,當P在P′點時,PA﹣PB=AB,此時線段AP與線段BP之差達到最大,求出直線AB于x軸的交點坐標即可.
解:∵把A(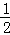 ,y1),B(2,y2)代入反比例函數y=
,y1),B(2,y2)代入反比例函數y= 得:y1=2,y2=
得:y1=2,y2=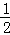 ,
,
∴A(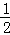 ,2),B(2,
,2),B(2,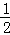 ),
),
∵在△ABP中,由三角形的三邊關系定理得:|AP﹣BP|<AB,
∴延長AB交x軸于P′,當P在P′點時,PA﹣PB=AB,
即此時線段AP與線段BP之差達到最大,
設直線AB的解析式是y=kx+b,
把A、B的坐標代入得: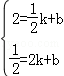 ,
,
解得:k=﹣1,b=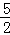 ,
,
∴直線AB的解析式是y=﹣x+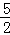 ,
,
當y=0時,x=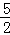 ,
,
即P(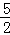 ,0),
,0),
故選D.
考點:反比例函數綜合題;待定系數法求一次函數解析式;三角形三邊關系.
點評:本題考查了三角形的三邊關系定理和用待定系數法求一次函數的解析式的應用,解此題的關鍵是確定P點的位置,題目比較好,但有一定的難度.


科目:初中數學 來源: 題型:
 如圖所示,已知等邊△ABC的邊長為a,P是△ABC內一點,PD∥AB,PE∥BC,PF∥AC,點D、E、F分別在BC、AC、AB上,猜想:PD+PE+PF=
如圖所示,已知等邊△ABC的邊長為a,P是△ABC內一點,PD∥AB,PE∥BC,PF∥AC,點D、E、F分別在BC、AC、AB上,猜想:PD+PE+PF=查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com