
【題目】已知函數y=﹣xm﹣1+bx﹣3(m,b為常數)是二次函數,其圖象的對稱軸為直線x=1
(I)求該二次函教的解析式;
(Ⅱ)當﹣2≤x≤0時,求該二次函數的函數值y的取值范圍.
【答案】(Ⅰ)該二次函教的解析式為y=﹣x2+2x﹣3;(Ⅱ)﹣11≤y≤﹣3.
【解析】
(Ⅰ)根據對稱軸方程,列式求出b的值,從而求得二次函數的解析式;
(Ⅱ)先由y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2知函數有最大值﹣2,然后求出x=﹣2和x=0時y的值即可得答案.
解:(Ⅰ)∵函數y=﹣xm﹣1+bx﹣3(m,b為常數)是二次函數其圖象的對稱軸為直線x=1,
∴m﹣1=2,![]() ,
,
∴m=3,b=2.
∴該二次函教的解析式為y=﹣x2+2x﹣3.
(Ⅱ)∵y=﹣x2+2x﹣3圖象的對稱軸為直線x=1,并且開口向下,
∴當﹣2≤x≤0時,y值在對稱軸的左邊,并且單調遞增,
當x=﹣2時,y=﹣11;
當x=0時,y=﹣3;
∴當﹣2≤x≤0時,求該二次函數的函數值y的取值范圍為﹣11≤y≤﹣3.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】2018年非洲豬瘟疫情暴發后,今年豬肉價格不斷走高,引起了民眾與政府的高度關注,據統計:今年7月20日豬肉價格比今年年初上漲了60%,某市民今年7月20日在某超市購買1千克豬肉花了80元錢.
(1)問:今年年初豬肉的價格為每千克多少元?
(2)某超市將進貨價為每千克65元的豬肉,按7月20日價格出售,平均一天能銷售出100千克,經調查表明:豬肉的售價每千克下降1元,其日銷售量就增加10千克,超市為了實現銷售豬內每天有1560元的利潤,并且可能讓顧客得到實惠,豬肉的售價應該下降多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)某學校“智慧方園”數學社團遇到這樣一個題目:
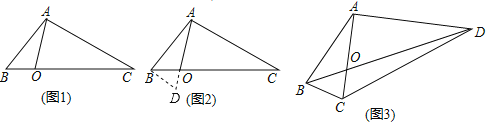
如圖1,在△ABC中,點O在線段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的長.
,BO:CO=1:3,求AB的長.
經過社團成員討論發現,過點B作BD∥AC,交AO的延長線于點D,通過構造△ABD就可以解決問題(如圖2).
請回答:∠ADB= °,AB= .
(2)請參考以上解決思路,解決問題:
如圖3,在四邊形ABCD中,對角線AC與BD相交于點O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的長.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“泥興陶,,是欽州的一張文化名片。欽州市某妮興陶公司以每只60元的價格銷售一種成本價為40元的文化紀念杯,每星期可售出100只。后來經過市場調查發現,每只杯子的售價每降低1元,則平均何星期可多買出10只。若該公司銷售這種文化紀念杯要想平均每星期獲利2240元,請回答:
(1)每只杯應降價多少元?
(2)在平均每星期獲利不變的情況下,為盡可能讓利于顧客,贏得市場,該公司應該按原售價的幾折出售?
查看答案和解析>>
科目:初中數學 來源: 題型:
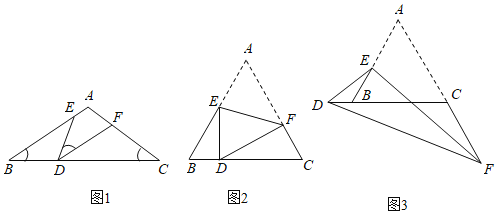
【題目】(1)模型探究:如圖1,D、E、F分別為△ABC三邊BC、AB、AC上的點,且∠B=∠C=∠EDF=a.△BDE與△CFD相似嗎?請說明理由;
(2)模型應用:△ABC為等邊三角形,其邊長為8,E為AB邊上一點,F為射線AC上一點,將△AEF沿EF翻折,使A點落在射線CB上的點D處,且BD=2.
①如圖2,當點D在線段BC上時,求![]() 的值;
的值;
②如圖3,當點D落在線段CB的延長線上時,求△BDE與△CFD的周長之比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2+bx+c經過點C(0,3),與x軸交于A,B兩點,點A(﹣1,0).
(I)求該拋物線的解析式;
(Ⅱ)D為拋物線對稱軸上一點,當△ACD的周長最小時,求點D的坐標;
(Ⅲ)在拋物線上是否存在一點P,使CP恰好將以A,B,C,P為頂點的四邊形的面積分為相等的兩部分?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
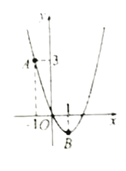
【題目】如圖,二次函數![]() 的圖象過點
的圖象過點![]() 、頂點
、頂點![]() 的橫坐標為.
的橫坐標為.
(1)求這個二次函數的解析式;
(2)點![]() 在該一次函數的圖象上,點
在該一次函數的圖象上,點![]() 在
在![]() 軸上,若以
軸上,若以![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的坐標。
的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦期間,某賓館有50個房間供游客居住,當每個房間每天的定價為180元時,房間會全部住滿;當每個房間每天的定價每增加10元時,就會有一個房間空閑.如果游客居住房間,賓館需對每個房間每天支出20元的各種費用.
(1)若房價定為200元時,求賓館每天的利潤;
(2)房價定為多少時,賓館每天的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1) 知識儲備
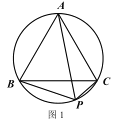
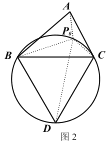
①如圖 1,已知點 P 為等邊△ABC 外接圓的弧BC 上任意一點.求證:PB+PC= PA.
②定義:在△ABC 所在平面上存在一點 P,使它到三角形三頂點的距離之和最小,則稱點 P 為△ABC
的費馬點,此時 PA+PB+PC 的值為△ABC 的費馬距離.
(2)知識遷移
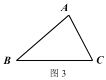
①我們有如下探尋△ABC (其中∠A,∠B,∠C 均小于 120°)的費馬點和費馬距離的方法:
如圖 2,在△ABC 的外部以 BC 為邊長作等邊△BCD 及其外接圓,根據(1)的結論,易知線段____的長度即為△ABC 的費馬距離.
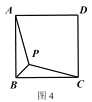
②在圖 3 中,用不同于圖 2 的方法作出△ABC 的費馬點 P(要求尺規作圖).
(3)知識應用
①判斷題(正確的打√,錯誤的打×):
ⅰ.任意三角形的費馬點有且只有一個(__________);
ⅱ.任意三角形的費馬點一定在三角形的內部(__________).
②已知正方形 ABCD,P 是正方形內部一點,且 PA+PB+PC 的最小值為![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
邊長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com