
【題目】如圖,已知拋物線![]() 經過點A(1,0)和B(0,3),其頂點為D.設P為該拋物線上一點,且位于拋物線對稱軸右側,作PH⊥對稱軸,垂足為H,若△DPH與△AOB相似
經過點A(1,0)和B(0,3),其頂點為D.設P為該拋物線上一點,且位于拋物線對稱軸右側,作PH⊥對稱軸,垂足為H,若△DPH與△AOB相似
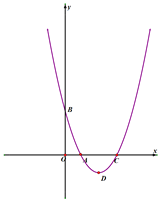
(1)求拋物線的解析式
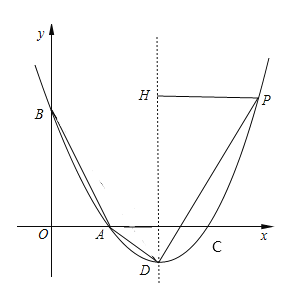
(2)求點P的坐標
【答案】(1)y=x2-4x+3;(2)(5,8)或(![]() ,-
,-![]() ).
).
【解析】
(1)利用待定系數法求拋物線解析式;
(2)設P(x,x2-4x+3)(x>2),則H(2,x2-4x+3),分別表示出PH和HD,分![]() 時,
時,![]() 時兩種情況分別求出x即可.
時兩種情況分別求出x即可.
解:(1)把A(1,0)和B(0,3)代入y=x2+bx+c得![]() ,解得
,解得![]() ,
,
∴拋物線解析式為y=x2-4x+3;
(2)拋物線的對稱軸為直線x=2,
設P(x,x2-4x+3)(x>2),則H(2,x2-4x+3),
∴PH=x-2,HD=x2-4x+3-(-1)=x2-4x+4,
∵∠PHD=∠AOB=90°,
∴當![]() 時,△PHD∽△AOB,即
時,△PHD∽△AOB,即![]() ,
,
解得x1=2(舍去),x2=5,此時P點坐標為(5,8);
當![]() 時,△PHD∽△BOA,即
時,△PHD∽△BOA,即![]() ,
,
解得x1=2(舍去),x2=![]() ,此時P點坐標為(
,此時P點坐標為(![]() ,-
,-![]() );
);
綜上所述,滿足條件的P點坐標為(5,8)或(![]() ,-
,-![]() ).
).


 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
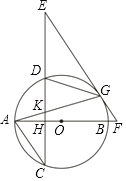
【題目】如圖,AB是⊙O的直徑,過圓外一點E作EF與⊙O相切于G,交AB的延長線于F,EC⊥AB于H,交⊙O于D,C兩點,連接AG交DC于K.
(1)求證:EG=EK;
(2)連接AC,若AC∥EF,cosC=![]() ,AK=
,AK=![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分8分)某商家預測一種應季襯衫能暢銷市場,就用13200元購進了一批這種襯衫,面市后果然供不應求.商家又用28800元購進了第二批這種襯衫,所購數量是第一批購進量的2倍,但單價貴了10元.
(1)該商家購進的第一批襯衫是多少件?
(2)若兩批襯衫按相同的標價銷售,最后剩下50件按八折優惠賣出,如果兩批襯衫全部售完后利潤率不低于25%(不考慮其它因素),那么每件襯衫的標價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鄂爾多斯市某百貨商場銷售某一熱銷商品A,其進貨和銷售情況如下:用16000元購進一批該熱銷商品A,上市后很快銷售一空,根據市場需求情況,該商場又用7500元購進第二批該商品,已知第二批所購件數是第一批所購件數的一半,且每件商品的進價比第一批的進價少10元.
(1)求商場第二批商品A的進價;
(2)商場同時銷售另一種熱銷商品B,已知商品B的進價與第二批商品A的進價相同,且最初銷售價為165元,每天能賣出125件,經市場銷售發現,若售價每上漲1元,其每天銷售量就減少5件,問商場該如何定售價,每天才能獲得最大利潤?并求出每天的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人分別加工100個零件,甲第1個小時加工了10個零件,之后每小時加工30個零件.乙在甲加工前已經加工了40個零件,在甲加工3小時后乙開始追趕甲,結果兩人同時完成任務.設甲、乙兩人各自加工的零件數為![]() (個),甲加工零件的時間為
(個),甲加工零件的時間為![]() (時),
(時),![]() 與
與![]() 之間的函數圖象如圖所示.
之間的函數圖象如圖所示.

(1)在乙追趕甲的過程中,求乙每小時加工零件的個數.
(2)求甲提高加工速度后甲加工的零件數![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(3)當甲、乙兩人相差12個零件時,直接寫出甲加工零件的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
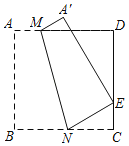
【題目】如圖,把正方形紙片ABCD沿對邊上的兩點M、N所在的直線對折,使點B落在邊CD上的點E處,折痕為MN,其中CE=![]() CD.若AB的長為2,則MN的長為( )
CD.若AB的長為2,則MN的長為( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
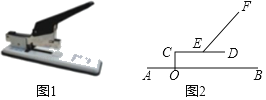
【題目】訂書機是由推動器、托板、壓形器、底座、定位軸等組成.如圖1是一臺放置在水平桌面上的大型訂書機,將其側面抽象成如圖2所示的幾何圖形.若壓形器EF的端點E固定于定位軸CD的中點處,在使用過程中,點D和點F隨壓形器及定位軸繞點C旋轉,CO⊥AB于點O,CD=12cm連接CF,若∠FED=45°,∠FCD=30°.
(1)求FC的長;
(2)若OC=2cm求在使用過程中,當點D落在底座AB上時,請計算CD與AB的夾角及點F運動的路線之長.(結果精確到0.1cm,參考數據:sin9.6°≈0.17.π≈3.14,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 為滿足社區居民健身的需要,市政府準備采購若干套健身器材免費提供給社區,經考察,勁松公司有![]() 兩種型號的健身器可供選擇.
兩種型號的健身器可供選擇.
(1)勁松公司2015年每套![]() 型健身器的售價為
型健身器的售價為![]() 萬元,經過連續兩年降價,2017年每套售價為
萬元,經過連續兩年降價,2017年每套售價為![]() 萬元,求每套
萬元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府經過招標,決定年內采購并安裝勁松公司![]() 兩種型號的健身器材共
兩種型號的健身器材共![]() 套,采購專項費總計不超過
套,采購專項費總計不超過![]() 萬元,采購合同規定:每套
萬元,采購合同規定:每套![]() 型健身器售價為
型健身器售價為![]() 萬元,每套
萬元,每套![]() 型健身器售價我
型健身器售價我![]() 萬元.
萬元.
①![]() 型健身器最多可購買多少套?
型健身器最多可購買多少套?
②安裝完成后,若每套![]() 型和
型和![]() 型健身器一年的養護費分別是購買價的
型健身器一年的養護費分別是購買價的![]() 和
和![]() .市政府計劃支出
.市政府計劃支出![]() 萬元進行養護.問該計劃支出能否滿足一年的養護需要?
萬元進行養護.問該計劃支出能否滿足一年的養護需要?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角頂點P1(3,3),P2,P3,…均在直線y=﹣![]() x+4上,設△P1OA1,△P2A1A2,△P3A2A3,…的面積分別為S1,S2,S3,…依據圖形所反映的規律,S2019=_____.
x+4上,設△P1OA1,△P2A1A2,△P3A2A3,…的面積分別為S1,S2,S3,…依據圖形所反映的規律,S2019=_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com