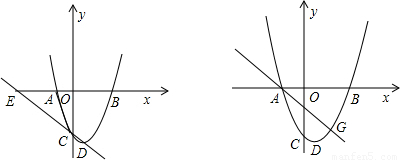分析:(1)求二次函數(shù)的表達(dá)式,需要求出A、B、C三點(diǎn)坐標(biāo).已知B點(diǎn)坐標(biāo),且OB=OC,可知C(0,3),tan∠ACO=
,則A坐標(biāo)為(-1,0).將A,B,C三點(diǎn)坐標(biāo)代入關(guān)系式,可求得二次函數(shù)的表達(dá)式.
(2)假設(shè)存在這樣的點(diǎn)F(m,n),已知拋物線關(guān)系式,求出頂點(diǎn)D坐標(biāo),今兒求出直線CD,E是直線與x軸交點(diǎn),可得E點(diǎn)坐標(biāo).四邊形AECF為平行四邊形,則CE∥AF,則兩直線斜率相等,可列等式(1),CE=AF,可列等式(2),F(xiàn)在拋物線上,為等式(3),根據(jù)這三個(gè)等式,即可求出m、n是否存在.
(3)分情況討論,當(dāng)圓在x軸上方時(shí),根據(jù)題意可知,圓心必定在拋物線的對稱軸上,設(shè)圓半徑為r,則N的坐標(biāo)為(r+1,r),將其代入拋物線解析式,可求出r的值.當(dāng)圓在x軸的下方時(shí),方法同上,只是N的坐標(biāo)變?yōu)椋╮+1,-r),代入拋物線解析式即可求解.
(4)G在拋物線上,代入解析式求出G點(diǎn)坐標(biāo),設(shè)點(diǎn)P的坐標(biāo)為(x,y),即(x,x
2-2x-3)已知點(diǎn)A、G坐標(biāo),可求出線段AG的長度,以及直線AG的解析式,再根據(jù)點(diǎn)到直線的距離求出P到直線的距離,即為三角形AGP的高,從而用x表示出三角形的面積,然后求當(dāng)面積最大時(shí)x的值.
解答: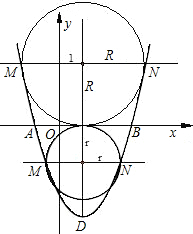
解:(1)方法一:由已知得:C(0,-3),A(-1,0)(1分)
將A、B、C三點(diǎn)的坐標(biāo)代入
得
(2分)
解得:
(3分)
所以這個(gè)二次函數(shù)的表達(dá)式為:y=x
2-2x-3(3分)
方法二:由已知得:C(0,-3),A(-1,0)(1分)
設(shè)該表達(dá)式為:y=a(x+1)(x-3)(2分)
將C點(diǎn)的坐標(biāo)代入得:a=1(3分)
所以這個(gè)二次函數(shù)的表達(dá)式為:y=x
2-2x-3(3分)
(注:表達(dá)式的最終結(jié)果用三種形式中的任一種都不扣分)
(2)方法一:存在,F(xiàn)點(diǎn)的坐標(biāo)為(2,-3)(4分)
理由:易得D(1,-4),
所以直線CD的解析式為:y=-x-3
∴E點(diǎn)的坐標(biāo)為(-3,0)(4分)
由A、C、E、F四點(diǎn)的坐標(biāo)得:AE=CF=2,AE∥CF
∴以A、C、E、F為頂點(diǎn)的四邊形為平行四邊形
∴存在點(diǎn)F,坐標(biāo)為(2,-3)(5分)
方法二:易得D(1,-4),所以直線CD的解析式為:y=-x-3
∴E點(diǎn)的坐標(biāo)為(-3,0)(4分)
∵以A、C、E、F為頂點(diǎn)的四邊形為平行四邊形
∴F點(diǎn)的坐標(biāo)為(2,-3)或(-2,-3)或(-4,3)
代入拋物線的表達(dá)式檢驗(yàn),只有(2,-3)符合
∴存在點(diǎn)F,坐標(biāo)為(2,-3)(5分)
(3)如圖,①當(dāng)直線MN在x軸上方時(shí),
設(shè)圓的半徑為R(R>0),則N(R+1,R),
代入拋物線的表達(dá)式,解得
R=(6分)
②當(dāng)直線MN在x軸下方時(shí),
設(shè)圓的半徑為r(r>0),
則N(r+1,-r),
代入拋物線的表達(dá)式,
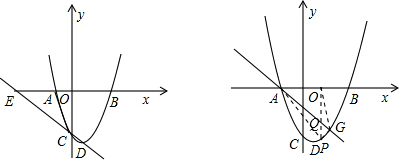
解得
r=(7分)
∴圓的半徑為
或
.(7分)
(4)過點(diǎn)P作y軸的平行線與AG交于點(diǎn)Q,
易得G(2,-3),直線AG為y=-x-1.(8分)
設(shè)P(x,x
2-2x-3),則Q(x,-x-1),
PQ=-x
2+x+2.S
△APG=S
△APQ+S
△GPQ=
(-x
2+x+2)×3(9分)
當(dāng)x=
時(shí),△APG的面積最大
此時(shí)P點(diǎn)的坐標(biāo)為(
,-
),S
△APG的最大值為
.(10分)


 解:(1)方法一:由已知得:C(0,-3),A(-1,0)(1分)
解:(1)方法一:由已知得:C(0,-3),A(-1,0)(1分)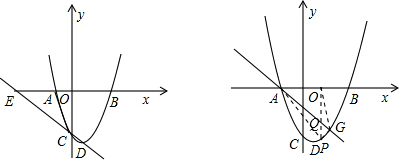


 優(yōu)學(xué)名師名題系列答案
優(yōu)學(xué)名師名題系列答案
 .
.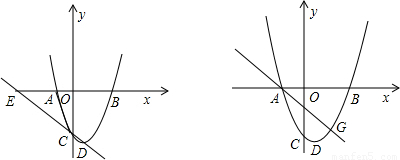
 .
.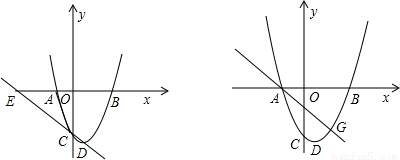
 .
.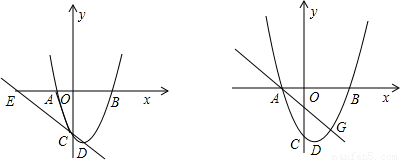
 .
.