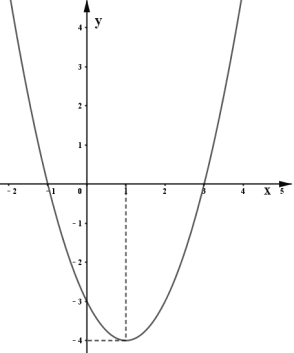
【題目】拋物線y＝ax2＋bx＋c的圖象如圖所示，根據圖象回答問題．
（1）直接寫出x滿足什么條件時，y隨x的增大而增大；
（2）直接寫出方程ax2＋bx＋c＝0的根；
（3）直接寫出不等式ax2＋bx＋c＜0 的解集；
（4）若方程ax2＋bx＋c＋k＝1沒有實數根，直接寫出k的取值范圍．
【答案】（1）
；（2）
，
；（3）
；（4）
．
【解析】
（1）根據函數圖象可知，時，y隨x的增大而增大，進行解答即可；
（2）根據函數圖象可知，方程的根，即為拋物線與x軸交點的橫坐標，進行解答即可；
（3）根據函數圖象可知，不等式ax2＋bx＋c＜0的解集為，進行解答即可；
（4）根據函數圖象可知，，方程ax2＋bx＋c＋k＝1無實數根，進行解答即可；
解：（1）觀察圖象可知，當時，y隨x的增大而增大；
（2）觀察圖象可知，方程ax2＋bx＋c＝0的根，即為拋物線與x軸交點的橫坐標，
∴，；
（3）觀察圖象可知：不等式ax2＋bx＋c＜0的解集為；
（4）由圖象可知，，方程ax2＋bx＋c＋k＝1無實數根；
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
經過點
，
，直線
：
交
軸于點
，且與拋物線交于
，
兩點，
為拋物線上一動點（不與，重合）.
（1）求拋物線的解析式；
（2）當點在直線下方時，過點作
軸交于點
，
軸交于點
，求
的最大值.
（3）設
為直線上的點，以，
，，為頂點的四邊形能否構成平行四邊形？若能，求出點的坐標；若不能，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
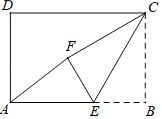
【題目】如圖，在矩形ABCD中，AB=3，CB=2，點E為線段AB上的動點，將△CBE沿CE折疊，使點B落在矩形內點F處，下列結論正確的是_____（寫出所有正確結論的序號）
①當E為線段AB中點時，AF∥CE；
②當E為線段AB中點時，AF=
；
③當A、F、C三點共線時，AE=
；
④當A、F、C三點共線時，△CEF≌△AEF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD中，G為BC邊上一點，BE⊥AG于E，DF⊥AG于F，連接DE．
（1）求證：△ABE≌△DAF；
（2）若AF=1，四邊形ABED的面積為6，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
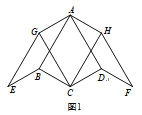
【題目】在四邊形 ABCD中，AB＝AD，∠BAD＝60°，邊BC繞點B順時針旋轉120°得到BE，邊DC繞點D逆時針旋轉120°得到DF，四邊形ABEG和四邊形ADFH為平行四邊形．
（1）如圖1，若BC＝CD，∠BCD＝120°，則∠GCH＝_______°；
（2）如圖2，若BC≠CD，探究∠GCH的大小是否發生變化，并證明你的結論；
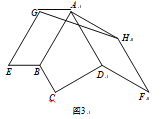
（3）如圖3，若∠BCD＝∠ADC＝90°，AB＝
請直接寫出△AGH的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，拋物線y＝ax2+2ax+c（a≠0）與x軸交于點A，B（1，0）兩點，與y軸交于點C，且OA＝OC．
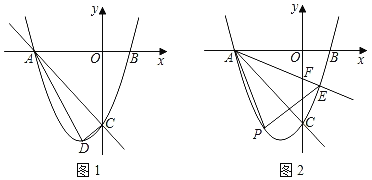
（1）求拋物線的解析式；
（2）點D是拋物線頂點，求△ACD的面積；
（3）如圖2，射線AE交拋物線于點E，交y軸的負半軸于點F（點F在線段AE上），點P是直線AE下方拋物線上的一點，S△ABE＝
，求△APE面積的最大值和此動點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】《九章算術》是中國傳統數學最重要的著作，在“勾股”章中有這樣一個問題：“今有邑方二百步，各中開門，出東門十五步有木，問：出南門幾步而見木？”
用今天的話說，大意是：如圖，
是一座邊長為200步（“步”是古代的長度單位）的正方形小城，東門
位于
的中點，南門
位于
的中點，出東門15步的
處有一樹木，求出南門多少步恰好看到位于處的樹木（即點
在直線
上）？請你計算
的長為__________步．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
