(1)連接OE、OF.
∵∠EOF=2∠EAF,∠EAF=45°,
∴∠EOF=90°;
∴△EOF是等腰直角三角形,
∴OE=

EF=2

,
∴直徑AP=2OE=4

;
(2)S
陰影=S
扇形EOF-S
△EOF=
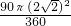
-

×2

×2

=2π-4;
(3)在三角形OEP中,根據(jù)垂徑定理和勾股定理知,當(dāng)OP取最小值時(shí),EF的值最小;又根據(jù)點(diǎn)到直線的距離垂線段最短垂線段最短知當(dāng)AP⊥BC時(shí),AP最短.
所以當(dāng)AP⊥BC時(shí),EF最短.
分析:(1)連接OE、OF構(gòu)建等腰直角三角形OEF,然后利用勾股定理求得AP的長度;
(2)利用扇形的面積公式和三角形的面積公式分別求得S
扇形EOF、S
△EOF的值;然后根據(jù)圖形的特點(diǎn)知:S
陰影=S
扇形EOF-S
△EOF;
(3)由垂徑定理知,當(dāng)AP最短時(shí),EF則取最小值;又根據(jù)點(diǎn)到直線的距離垂線段最短垂線段最短知當(dāng)AP⊥BC時(shí),AP最短.
點(diǎn)評:考查了同學(xué)們綜合利用垂徑定理、圓周角定理、等腰直角三角形的判定與性質(zhì)解決問題的能力,有利于培養(yǎng)同學(xué)們的發(fā)散思維能力.

 在△ABC中,P是BC邊上的一個(gè)動點(diǎn),以AP為直徑的⊙O分別交AB、AC于點(diǎn)E和點(diǎn)F.
在△ABC中,P是BC邊上的一個(gè)動點(diǎn),以AP為直徑的⊙O分別交AB、AC于點(diǎn)E和點(diǎn)F. (1)連接OE、OF.
(1)連接OE、OF. EF=2
EF=2 ,
, ;
;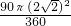 -
- ×2
×2 ×2
×2 =2π-4;
=2π-4;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案