
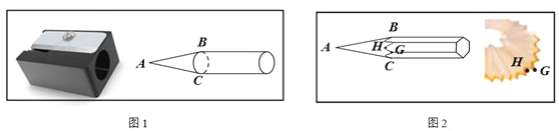
【題目】已知如圖1,圓柱體鉛筆插入卷筆刀充分卷削,得到底面直徑BC為2的圓錐,∠BAC=30°.底面邊長為1的正六棱柱鉛筆插入卷削,得到如圖2所示鉛筆和鋸齒狀木屑(木屑厚度忽略不計),木屑鋸齒齒鋒點G相鄰凹陷最低點為H,則AG=________,GH=________.
【答案】![]()
![]()
【解析】
抽象圖形,利用等腰三角形的性質和三角形外角的性質,可證得∠GEO=30°,再結合已知條件求出OG,EG的長,利用解直角三角形求出EO的長,從而可求出OA的長,然后利用勾股定理求出AG的長;底面邊長為1的正六棱柱鉛筆插入卷削,如圖,可得到△OGK是等邊三角形,利用解直角三角形求出OM,MN的長,再利用平行線分線段成比例定理可求出MH的長,然后證明△HMG是等腰直角三角形,繼而可求出HG的長.
解:如圖,
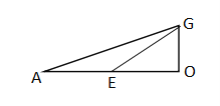
∵∠BAC=30°,
∴∠GAO=15°,
∵AE=EG,
∴∠GAO=∠AGE=15°
∴∠GEO=∠AGE+∠GAO=30°,
∵圓錐的底面直徑為2,
∴OG=1,
在Rt△AOG中,EG=2OG=2,
∴EO=EGcos∠GEO=2×cos30°=![]() ,
,
∴OA=AE+OE=2+![]() ,
,
∴![]() ;
;
∵底面邊長為1的正六棱柱鉛筆插入卷削,如圖,
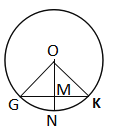
∴△OGK是邊長為1的等邊三角形,
∴OM=OGsin60°=![]() ,
,
∴MN=1-![]() ,
,
如圖,
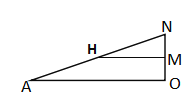
∵MH∥AO,
∴![]() ,
,
∴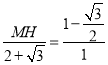 ,
,
解之:MH=![]() ,
,
∵GK=1,HG=HK,HM⊥GK,
∴△HKG是等腰直角三角形,
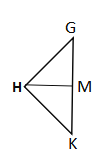
∴△HMG是等腰直角三角形,
∴![]() 即
即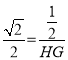 ,
,
解之:HG=![]() .
.
故答案為:![]() ;
;![]() .
.
此題考查正多邊形和圓,勾股定理,等邊三角形的判定及性質,等腰直角三角形的性質,平行線分線段成比例,解直角三角形,正確理解題中各部分之間的關系,根據題意畫出對應的圖形輔助解題是關鍵,體現數形結合是思想.


科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,D為直線BC上一點,E為直線AC上一點,
,D為直線BC上一點,E為直線AC上一點,![]() ,設
,設![]() ,
,![]() .
.
(1)如圖1,若點D在線段C上,點E在線段AC上,![]() ,
,![]() ,則
,則![]() ______
______![]() ;
;![]() ________
________![]() .
.
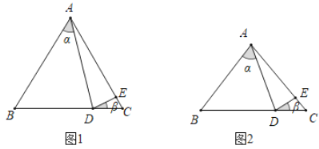
(2)如圖2,若點D在線段BC上,點E在線段AC上,則![]() ,
,![]() 之間有什么關系式?它說明理由.
之間有什么關系式?它說明理由.
(3)是否存在不同于(2)中的![]() ,
,![]() 之間的關系式?請寫出這個關系式(寫出一種即可),說明理由:若不存在,請說明理由.
之間的關系式?請寫出這個關系式(寫出一種即可),說明理由:若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一”小長假期間,小李一家想到以下四個5A級風景區旅游:A.石林風景區;B.香格里拉普達措國家公園;C.騰沖火山地質公園;D.玉龍雪山景區.但因為時間短,小李一家只能選擇其中兩個景區游玩
(1)若小李從四個景區中隨機抽出兩個景區,請用樹狀圖或列表法求出所有可能的結果;
(2)在隨機抽出的兩個景區中,求抽到玉龍雪山風景區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
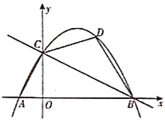
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若點![]() 是拋物線上的一點,且位于直線
是拋物線上的一點,且位于直線![]() 上方,連接
上方,連接![]() ,
,![]() ,
,![]() .當四邊形
.當四邊形![]() 的面積有最大值時,求點
的面積有最大值時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠ACB=90°,AB=![]() .點D,E分別在邊AB,AC上,將線段ED繞點E按逆時針方向旋轉90°得到EF,連結BF,BF的中點為G.
.點D,E分別在邊AB,AC上,將線段ED繞點E按逆時針方向旋轉90°得到EF,連結BF,BF的中點為G.
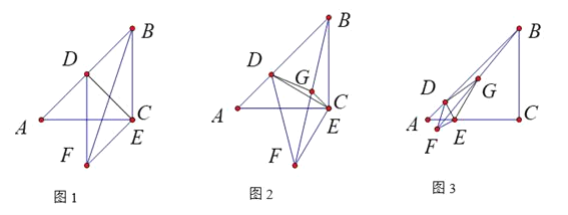
(1)當點E與點C重合時.
①如圖1,若AD=BD,求BF的長.
②當點D從點A運動到點B時,求點G的運動路徑長.
(2)當AE=3,點G在△DEF一邊所在直線上時,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
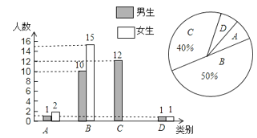
【題目】我縣實施新課程改革后,學生的自主字習、合作交流能力有很大提高.某學校為了了解學生自主學習、合作交流的具體情況,對部分學生進行了為期半個月的跟蹤調査,并將調査結果分類,A:特別好;B:好;C:一般;D:較差.現將調査結果繪制成以下兩幅不完整的統計圖,請你根據統計圖解答下列問題:
(1)本次調查中,一共調査了 名同學,其中C類女生有 名;
(2)將下面的條形統計圖補充完整;
(3)為共同進步,學校想從被調査的A類和D類學生中分別選取一位同學進行一幫一互助學習,請用列表法或畫樹形圖的方法求出所選兩位同學恰好是一位男生、一位女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=4,M是AD的中點,點E是線段AB上一動點,連接EM并延長交線段CD的延長線于點F.
(1)如圖1,求證:AE=DF;
(2)如圖2,若AB=2,過點M作MG⊥EF交線段BC于點G,判斷△GEF的形狀,并說明理由;
(3)如圖3,若AB=![]() ,過點M作MG⊥EF交線段BC的延長線于點G.
,過點M作MG⊥EF交線段BC的延長線于點G.
①直接寫出線段AE長度的取值范圍;
②判斷△GEF的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
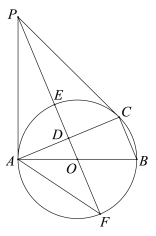
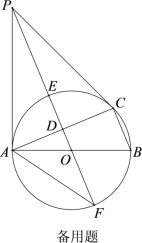
【題目】如圖,⊙O是△ABC的外接圓,AB是直徑,D是AC中點,直線OD與⊙O相交于E,F兩點,P是⊙O外一點,P在直線OD上,連接PA,PC,AF,且滿足∠PCA=∠ABC.
(1)求證:PA是⊙O的切線;
(2)證明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的長.
,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com