
【題目】 如圖,將小旗ACDB放于平面直角坐標系中,得到各頂點的坐標為A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以點B為旋轉中心,在平面直角坐標系內將小旗順時針旋轉90°. 
(1)畫出旋轉后的小旗A′C′D′B′;
(2)寫出點A′,C′,D′的坐標;
(3)求出線段BA旋轉到B′A′時所掃過的扇形的面積.
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=90°,AD⊥BC,垂足為D.
(1)求作∠ABC的平分線(要求:尺規作圖,保留作圖痕跡,不寫作法);
(2)若∠ABC的平分線分別交AD,AC于P,Q兩點,證明:AP=AQ.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】生活經驗表明,靠墻擺放梯子時,若梯子底端離墻的距離約為梯子長度的![]() ,則梯子比較穩定,如圖,AB為一長度為6米的梯子.
,則梯子比較穩定,如圖,AB為一長度為6米的梯子.
(1)當梯子穩定擺放時,它的頂端能達到5.7米高的墻頭嗎?
(2)如圖2,若梯子底端向左滑動(3![]() ﹣2)米,那么梯子頂端將下滑多少米?
﹣2)米,那么梯子頂端將下滑多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某旅游景區上山的一條小路上,有一些斷斷續續的臺階.下圖是其中的甲、乙兩段臺階路的示意圖.請你用所學過的有關統計知識(平均數、中位數、方差和極差)回答下列問題:
(1)兩段臺階路有哪些相同點和不同點?
(2)哪段臺階路走起來更舒服?為什么?
(3)為方便游客行走,需要重新整修上山的小路.對于這兩段臺階路,在臺階數不變的情況下,請你提出合理的整修建議.
圖中的數字表示每一級臺階的高度(單位:cm),并且數據15,16,16,14,14,15的方差s甲2=![]() ,數據11,15,18,17,10,19的方差s乙2=
,數據11,15,18,17,10,19的方差s乙2=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+c(a≠0)經過C(2,0),D(0,﹣1)兩點,并與直線y=kx交于A、B兩點,直線l過點E(0,﹣2)且平行于x軸,過A、B兩點分別作直線l的垂線,垂足分別為點M、N.
(1)求此拋物線的解析式;
(2)求證:AO=AM;
(3)探究:
①當k=0時,直線y=kx與x軸重合,求出此時 ![]() +
+ ![]() 的值;
的值;
②試說明無論k取何值, ![]() +
+ ![]() 的值都等于同一個常數.
的值都等于同一個常數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,其圖象反映的過程是:張強從家去體育場,在那里鍛煉了一陣后又走到文具店去買筆,然后散步走回家,其中x表示時間,y表示張強離家的距離.根據圖象,下列回答正確的是( )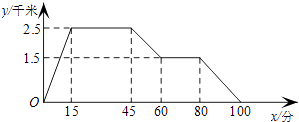
A.張強在體育場鍛煉45分鐘
B.張強家距離體育場是4千米
C.張強從離家到回到家一共用了200分鐘
D.張強從家到體育場的平均速度是10千米/小時
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△AOB中,∠AOB=90°,AO=6厘米,BO=8厘米,分別以OB和OA所在直線為x軸,y軸建立平面直角坐標系,如圖所示,動點M從點A開始沿AO方向以2厘米/秒的速度向點O移動,同時動點N從點O開始沿OB方向以4厘米/秒的速度向點B移動(其中一點到達終點時,另一點隨即停止移動).
(1)求過點A和點B的直線表達式;
(2)當點M移動多長時間時,四邊形AMNB的面積最小?并求出四邊形AMNB面積的最小值;
(3)在點M和點N移動的過程中,是否存在以O,M,N為頂點的三角形與△AOB相似?若存在,請求出點M 和點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】瑤寨中學食堂為學生提供了四種價格的午餐供其選擇,這四種價格分別是:A.3元,B.4元,C.5元,D.6元.為了了解學生對四種午餐的購買情況,學校隨機抽樣調查了甲、乙兩班學生某天購買四種午餐的情況,依據統計數據制成如下的統計圖表:
甲、乙兩班學生購買午餐的情況統計表
品種 | A | B | C | D |
甲 | 6 | 22 | 16 | 6 |
乙 | ? | 13 | 25 | 3 |

(1)求乙班學生人數;
(2)求乙班購買午餐費用的中位數;
(3)已知甲、乙兩班購買午餐費用的平均數為4.44元,從平均數和眾數的角度解答,哪個班購買的午餐價格較高?
(4)從這次接受調查的學生中,隨機抽查一人,恰好是購買C種午餐的學生的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com