
 如圖,一種零件的橫截面由三角形、矩形、扇形組成,其中∠BOA=60°,AD=25mm,半徑AO=10mm,求該零件的橫截面積.
如圖,一種零件的橫截面由三角形、矩形、扇形組成,其中∠BOA=60°,AD=25mm,半徑AO=10mm,求該零件的橫截面積.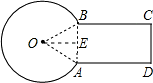 解:∵OB=OA,∠BOA=60°,
解:∵OB=OA,∠BOA=60°, ∠BOA=
∠BOA= ×60°=30°;
×60°=30°; mm,
mm, AB•OE+
AB•OE+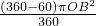 =25mm×10mm+
=25mm×10mm+ ×10mm×5
×10mm×5 mm+
mm+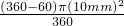 =250+25
=250+25 +
+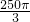 (mm2).
(mm2).

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com