【題目】如圖，△ABC中，∠CAB＝70°，在同一平面內(nèi)，將△ABC繞點A旋轉(zhuǎn)到△AB'C'的位置，使得C′C∥AB，則∠CAB'等于（ ）
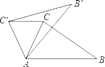
A. 30°B. 25°C. 15°D. 10°
【答案】A
【解析】
先根據(jù)平行線的性質(zhì)得∠ACC′＝∠CAB＝70°，再根據(jù)旋轉(zhuǎn)的性質(zhì)得AC＝AC′，∠CAC′＝∠BAB′，根據(jù)等腰三角形的性質(zhì)和三角形內(nèi)角和計算出∠CAC′＝40°，所以∠BAB′＝40°，然后計算∠CAB′＝∠CAB﹣∠BAB′即可．
解：∵C′C∥AB，
∴∠ACC′＝∠CAB＝70°，
∵△ABC繞點A旋轉(zhuǎn)到△AB'C'的位置，
∴AC＝AC′，∠CAC′＝∠BAB′，
∴∠ACC′＝∠AC′C＝70°，
∴∠CAC′＝180°﹣70°﹣70°＝40°，
∴∠BAB′＝40°，
∴∠CAB′＝∠CAB﹣∠BAB′＝70°﹣40°＝30°．
故選：A．
科目：初中數(shù)學 來源： 題型：
【題目】如圖，△ABC中，AD⊥BC于D，下列條件：①∠B+∠DAC=90°；②∠B=∠DAC；③
=
；④AB2=BDBC．其中一定能夠判定△ABC是直角三角形的有（ ）
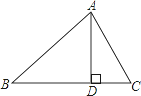
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】設
是不小于
的實數(shù)，關(guān)于
的方程
有兩個不相等的實數(shù)根
、
，
（1）求的取值范圍；
（2）若
，求值；
（3）求
的最大值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】在矩形紙片ABCD中，AB=6，BC=8．
（1）將矩形紙片沿BD折疊，點A落在點E處（如圖①），設DE與BC相交于點F，求BF的長；
（2）將矩形紙片折疊，使點B與點D重合（如圖②），求折痕GH的長．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】（閱讀）如圖1，四邊形
中，
，
，
，
，經(jīng)過點
的直線
將四邊形分成兩部分，直線與
所成的角設為
，將四邊形的直角
沿直線折疊，點
落在點
處，我們把這個操作過程記為
．
（理解）若點與點
重合，則這個操作過程為
[__________，__________]；
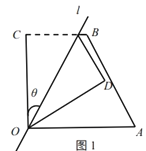
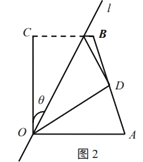
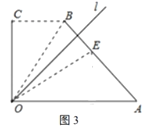
（嘗試）
（1）若點恰為
的中點(如圖2)，求；
（2）經(jīng)過
操作，點
落在
處，若點在四邊形的邊上(如圖3)，求出
的值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)y=-x 2 +2mx-m 2+4
(1)當m=1時，拋物線的對稱軸和頂點坐標:
(2)求證:不論m取何值時該二次函數(shù)的圖像與x軸必有兩個不同交點
(3)若該二次函數(shù)的圖像與x軸交于點A， B(點Ａ在點Ｂ的左側(cè))，頂點為C，則這時△ＡBC的面積為
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，如果點
，點
為某個菱形的一組對角的頂點，且點
在直線
上，那么稱該菱形為點的“伴隨菱形”，下圖為點的“伴隨菱形”的一個示意圖．
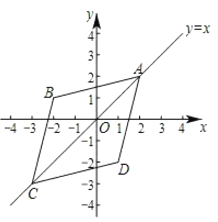
已知點
的坐標為(1，1)，點
的坐標為
．
（1）點
中，能夠成為點
的“伴隨菱形”的頂點的是__________________；
（2）如果四邊形
是點
的“伴隨菱形”．
①當點
的坐標為
時，求四邊形的面積；
②當四邊形中較小內(nèi)角的度數(shù)為60°時，求四邊形的面積；
③當四邊形的面積為8，且與直線
有公共點時，直接寫出
的取值范圍．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖所示的二次函數(shù)
的圖象中，觀察得出了下面五條信息：
①
；②
；③
；④
；⑤
，
你認為其中正確信息的個數(shù)有__________________個.
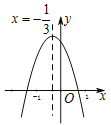
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】對x，y定義一種新運算x[]y=
（其中a，b均為非零常數(shù)），這里等式右邊是通常的四則混合運算，例如：0[]2=
=﹣2b．已知1[]2=3，﹣1[]3=﹣2．請解答下列問題．
(1)求a，b的值；
(2)若M=（m2﹣m﹣1）[]（2m﹣2m2），則稱M是m的函數(shù)，當自變量m在﹣1≤m≤3的范圍內(nèi)取值時，函數(shù)值M為整數(shù)的個數(shù)記為k，求k的值；
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com