Question

如圖，C島在A島的北偏東45°方向，在B島的北偏西25°方向．
（1）從C島看A，B兩島的視角∠ACB的度數是______．
（2）測量發現∠BAC=20°，A島與C島之間的距離AC為20海里，求A島與B島之間的距離，（結果精確到0.1海里）（參考數據：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）

Answer 1

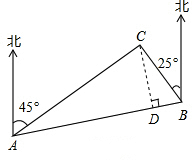
解：（1）∵兩正北方向平行，
∴∠CAB+∠CBA=180°-45°-25°=110°，
∴∠C=180°-110°=70°，

（2）作CD⊥AB于點D，
∵∠BAC=20°，AC=20海里，
∴CD=AC•sin20°≈20×0.342=6.84海里，AD=AC•cos20°≈20×0.940=18.8海里
∵∠C=70°，
∴∠BCD=20°，
∴DB=CD•tan20°≈6.84×0.364=2.49
∴AB=AD+DB=18.8+2.49≈21.3海里，
∴A島與B島之間的距離21.3海里．
故答案為：70．
分析：（1）根據兩直線平行，同旁內角相等求得∠C的度數即可；
（2）作CD⊥AB于點D，分別求得線段AD和線段DB的長，從而求得線段AB的長．
點評：本題考查了方向角問題，解題的關鍵是從實際問題中整理出直角三角形模型，并利用解直角三角形求解．