
我們知道:將一條線段AB分割成大小兩條線段AC、CB,若小線段CB與大線段AC的長度之比等于大線段AC與線段AB的長度之比,即![]() 這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.
這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.
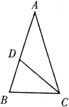
(1)類似地我們可以定義,頂角為36°的等腰三角形叫黃金三角形,其底與腰之比為黃金數,底角平分線與腰的交點為腰的黃金分割點.如圖,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分線CD交腰AB于點D,請你說明D為腰AB的黃金分割點的理由.
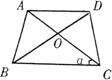
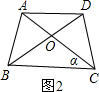
(2)若腰和上底相等,對角線和下底相等的等腰梯形叫作黃金梯形,其對角線的交點為對角線的黃金分割點.如圖,AD∥BC,AB=AD=DC,AC=BD=BC,試說明O為AC的黃金分割點.
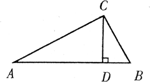
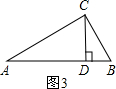
(3)如圖,在Rt△ABC中,∠ACB=90°,CD為斜邊AB上的高,∠A、∠B、∠ACB的對邊分別為a、b、c.若D是AB的黃金分割點,那么a、b、c之間的數量關系是什么?并證明你的結論.
|
(1)證明:在△ABC中,∵∠A=36°,AB=AC ∴∠ACB= ∵CD為∠ACB的角平分線,∴∠DCB= 又∵∠ABC=∠CBD ∴△ABC∽△CBD ∴ ∵∠ABC=∠ACB=72° ∴∠BDC=∠ABC=72°∴BC=CD同理可證,AD=CD ∴BC=DC=AD,∴ ∴D為腰AB的黃金分割點.
(2)證明:在△ABC和△DCB中,∵AB=DC,AD∥BC,∴∠ABC=∠DCB.又∵BC=BC,∴△ABC≌△DCB. ∴∠ACB=∠DBC=α ∵AD∥BC,∴∠DBC=∠BDA=α ∵AB=AD∴∠ABD=∠BDA=α ∴∠ABC=2α.∵AC=BC,∴∠ABC=∠CAB=2α 在△ABC中,∵∠ABC+∠ACB+∠BAC=180° ∴5α=180°∴α=36°在等腰△ABC中 ∵BO為∠ABC的角平分線,∠ACB=α=36°∴O為腰AC的黃金分割點, 即
(3)a、b、c之間的數量關系是b2=ac. ∵∠ACB=90°,CD⊥AB ∴∠ACB=∠ADC=90° ∵∠A=∠A∴△ACB∽△ADC∴ ∴b2=AD·c同理可證,a2=BD·c∴AD= ①BD= ②又∵D為AB的黃金分割點,∴AD2=BD·c ③把①、②代入③得b4=a2c2∵a、c均為正數,∴b2=ac ∴a、b、c之間的數量關系為b2=ac.
|


科目:初中數學 來源: 題型:
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
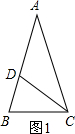
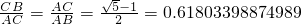 .這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.類似地我們可以定義,頂角為36°的等腰三角形叫黃金三角形,其底與腰之比為黃金數,底角平分線與腰的交點為腰的黃金分割點.
.這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.類似地我們可以定義,頂角為36°的等腰三角形叫黃金三角形,其底與腰之比為黃金數,底角平分線與腰的交點為腰的黃金分割點.


查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源:2008年北京市大興區中考數學二模試卷(解析版) 題型:解答題
 .這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.類似地我們可以定義,頂角為36°的等腰三角形叫黃金三角形,其底與腰之比為黃金數,底角平分線與腰的交點為腰的黃金分割點.
.這種分割稱為黃金分割,點C叫做線段AB的黃金分割點.類似地我們可以定義,頂角為36°的等腰三角形叫黃金三角形,其底與腰之比為黃金數,底角平分線與腰的交點為腰的黃金分割點.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com