
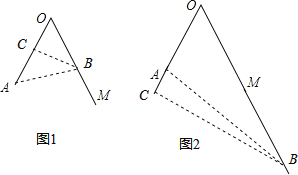
【題目】如圖,已知∠AOM=60°,在射線OM上有點B,使得AB與OB的長度都是整數,由此稱B是“和諧點”,若OA=8,當B為“和諧點”時,AB和OB的長分別為_____________.

【答案】![]() 或
或![]() 或
或![]() 或
或![]() .(AB=x,OB=y)
.(AB=x,OB=y)
【解析】試題解析:過點B作BC⊥OA,交OA于點C,連接AB,可能有兩種情況,垂足在OA上或者垂足在OA延長線上.
設OB=y,AB=x,
∵∠AOM=60°,
∴OC=OBcos60°=![]() y,
y,
∴AC=OA-OC=8-![]() y或AC=OC-OA=
y或AC=OC-OA=![]() y -8,
y -8,
∵BC2=OB2-OC2,BC2=AB2-AC2,
∴y2-(![]() y)2=x2-(8-
y)2=x2-(8-![]() y)2或x2-(
y)2或x2-(![]() y -8)2=y2-(
y -8)2=y2-(![]() y)2,
y)2,
∴x2-(y-4)2=48,
∵x與y是正整數,且y必為正整數,x-4為大于等于-4的整數,
將原方程轉為 X2-Y2=48,先求(X+Y)(X-Y)=48的正整數解,
∵(X+Y)和(X-Y)同奇同偶,
∴(X+Y)和(X-Y)同為偶數;
∴X2-Y2=48可能有幾組正整數解:
![]() ,
, ![]() ,
, ![]() ,
,
解得: ![]() ,
, ![]() ,
, ![]() ,
,
∴x的可能值有3個:x=7,x=8或x=13,
當x=7時,y-4=±1,y=3或y=5;
當x=8時,y-4=±4,y=8或y=0(舍去);
當x=13時,y-4=±11,y=15或y=-7(舍去);
∴共有4組解: ![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知點E、F在直線AB上,點G在線段CD上,ED與FG交于點H,∠C=∠EFG,∠CED=∠GHD. 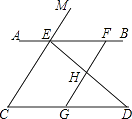
(1)求證:CE∥GF;
(2)試判斷∠AED與∠D之間的數量關系,并說明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com