
【題目】![]() 指居民消費價格指數,反映居民家庭購買消費商品及服務的價格水平的變動情況.
指居民消費價格指數,反映居民家庭購買消費商品及服務的價格水平的變動情況. ![]() 的漲跌率在一定程度受到季節性因素和天氣因素的影響.根據北京市
的漲跌率在一定程度受到季節性因素和天氣因素的影響.根據北京市![]() 年與
年與![]() 年
年![]() 漲跌率的統計圖中的信息,請判斷
漲跌率的統計圖中的信息,請判斷![]() 年
年![]() ~
~![]() 月份與
月份與![]() 年
年![]() ~
~![]() 月份,同月份比較
月份,同月份比較![]() 漲跌率下降最多的月份是__________月;請根據圖中提供的信息,預估北京市
漲跌率下降最多的月份是__________月;請根據圖中提供的信息,預估北京市![]() 年第四季度
年第四季度![]() 漲跌率變化趨勢是__________,你的預估理由是__________;
漲跌率變化趨勢是__________,你的預估理由是__________;
【答案】 8 先減后增 ![]() 年9~12月份
年9~12月份 ![]() 漲跌率先減后增,預估北京市
漲跌率先減后增,預估北京市![]() 年第四季度
年第四季度![]() 漲跌率變化趨勢是先減后增
漲跌率變化趨勢是先減后增
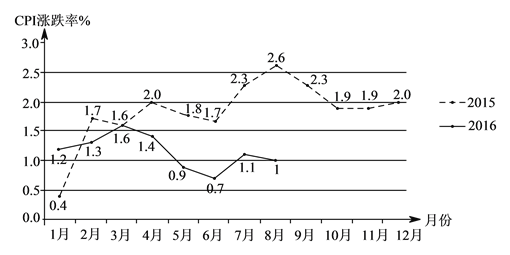
【解析】試題解析:由函數圖象可知,2015年18月份與2016年18月份,同月份CPI漲跌率8月份相差2.6%1%=1.6%,
∴同月份比較CPI漲跌率下降最多的月份是8月;
根據圖中提供的信息,預估北京市2016年第四季度CPI漲跌率變化趨勢是先減后增,
預估理由是2015年18月份與2016年18月份,同月份CPI漲跌率基本保持一致,而2015年912月份CPI漲跌率先減后增,
∴預估北京市2016年第四季度CPI漲跌率變化趨勢是先減后增,
故答案為:8,先減后增,2015年912月份CPI漲跌率先減后增,所以預估北京市2016年第四季度CPI漲跌率變化趨勢是先減后增.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,E為AC邊的中點,過點A作AD⊥AB交BE的延長線于點D,CG平分∠ACB交BD于點G.F為AB邊上一點,連接CF,且∠ACF=∠CBG.
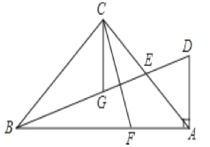
(1)求證:BG=CF;
(2)求證:CF=2DE;
(3)若DE=1,求AD的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(背景知識)
數軸是初中數學的一個重要工具,利用數軸可以將數與形完美結合.研究數軸我們發現有許多重要的規律:
例如,若數軸上![]() 點、
點、![]() 點表示的數分別為
點表示的數分別為![]() 、
、![]() ,則
,則![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ,線段
,線段![]() 的中點
的中點![]() 表示的數為
表示的數為![]() .
.
(問題情境)
在數軸上,點![]() 表示的數為-20,點
表示的數為-20,點![]() 表示的數為10,動點
表示的數為10,動點![]() 從點
從點![]() 出發沿數軸正方向運動,同時,動點
出發沿數軸正方向運動,同時,動點![]() 也從點
也從點![]() 出發沿數軸負方向運動,已知運動到4秒鐘時,
出發沿數軸負方向運動,已知運動到4秒鐘時,![]() 、
、![]() 兩點相遇,且動點
兩點相遇,且動點![]() 、
、![]() 運動的速度之比是
運動的速度之比是![]() (速度單位:單位長度/秒).
(速度單位:單位長度/秒).
![]()
![]()
備用圖
(綜合運用)
(1)點![]() 的運動速度為______單位長度/秒,點
的運動速度為______單位長度/秒,點![]() 的運動速度為______單位長度/秒;
的運動速度為______單位長度/秒;
(2)當![]() 時,求運動時間;
時,求運動時間;
(3)若點![]() 、
、![]() 在相遇后繼續以原來的速度在數軸上運動,但運動的方向不限,我們發現:隨著動點
在相遇后繼續以原來的速度在數軸上運動,但運動的方向不限,我們發現:隨著動點![]() 、
、![]() 的運動,線段
的運動,線段![]() 的中點
的中點![]() 也隨著運動.問點
也隨著運動.問點![]() 能否與原點重合?若能,求出從
能否與原點重合?若能,求出從![]() 、
、![]() 相遇起經過的運動時間,并直接寫出點
相遇起經過的運動時間,并直接寫出點![]() 的運動方向和運動速度;若不能,請說明理由.
的運動方向和運動速度;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
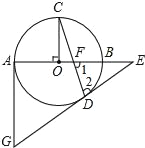
【題目】如圖的⊙O中,AB為直徑,OC⊥AB,弦CD與OB交于點F,過點D、A分別作⊙O的切線交于點G,并與AB延長線交于點E.
(1)求證:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半徑為3,求AG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示.
(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度數;
(2)∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠MON的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A從原點出發沿數軸向左運動,同時,點B也從原點出發沿數軸向右運動,3秒后,兩點相距15個單位長度.已知點B的速度是點A的速度的4倍(速度單位:單位長度/秒).
![]()
(1)求出點A、點B運動的速度,并在數軸上標出A、B兩點從原點出發運動3秒時的位置;
(2)若A、B兩點從(1)中的位置開始,仍以原來的速度同時沿數軸向左運動,幾秒時,原點恰好處在點A、點B的正中間?
(3)若A、B兩點從(1)中的位置開始,仍以原來的速度同時沿數軸向左運動時,另一點C同時從B點位置出發向A點運動,當遇到A點后,立即返回向B點運動,遇到B點后又立即返回向A點運動,如此往返,直到B點追上A點時,C點立即停止運動.若點C一直以20單位長度/秒的速度勻速運動,那么點C從開始運動到停止運動,行駛的路程是多少個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校八年級學生舉行朗誦比賽,全年級學生都參加,學校對表現優異的學生進行表彰,設置—、二、三等獎和進步獎共四個獎項,賽后將八年級(1)班的獲獎情況繪制成如圖所示的兩幅不完整的統計圖,請報據圖中的信息,解答下列問題:

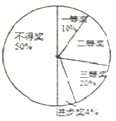
(1)八年級(1)班共有 名學生;
(2)將條形圖補充完整;在扇形統計圖中,“二等獎”對應的扇形的圓心角度數 ;
(3)如果該八年級共有800名學生,請估計榮獲一、二、三等獎的學生共有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
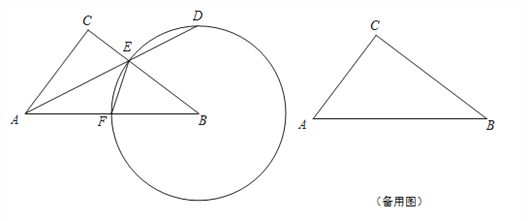
【題目】如圖,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,點F在線段AB上,以點B為圓心,BF為半徑的圓交BC于點E,射線AE交圓B于點D(點D、E不重合).
(1)如果設BF = x,EF = y,求y與x之間的函數關系式,并寫出它的定義域;
(2)如果![]() ,求ED的長;
,求ED的長;
(3)聯結CD、BD,請判斷四邊形ABDC是否為直角梯形?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平整的地面上,由若干個完全相同的棱長為 10 cm 的小正方體堆成一個幾何體,如圖 所示.
(1)這個幾何體由多少個小正方體組成?請畫出這個幾何體的三視圖.
(2)如果在這個幾何體的表面(不包括底面)噴上黃色的漆,則在所有的小正方體中,有多少個只有一個面是黃色?有多少個只有兩個面是黃色?有多少個只有三個面是黃色?
(3)假設現在你手里還有一些相同的小正方體,保持這個幾何體的主視圖、俯視圖形狀 不變,最多可以再添加幾個小正方體?這時如果要重新給這個幾何體表面(不包括底面) 噴上紅色的漆,需要噴漆的面積比原幾何體增加了還是減少了?增加或減少的面積是 多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com