

 ;(3)①若四邊形PMNQ為平行四邊形時,點P坐標為
;(3)①若四邊形PMNQ為平行四邊形時,點P坐標為 ,②若四邊形PMNQ為等腰梯形時,點P坐標 為
,②若四邊形PMNQ為等腰梯形時,點P坐標 為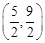 .
.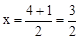 .
.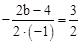 ,c-5=4,解得 b=2,c=9.
,c-5=4,解得 b=2,c=9. .
. ,點N坐標是
,點N坐標是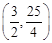 ,∴MN=
,∴MN=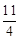 .
.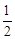 ,x2=
,x2=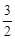 ,
,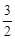 時,點P′與點M重合;
時,點P′與點M重合;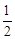 時,點P的坐標是
時,點P的坐標是 .
.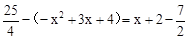 ,解得:x=
,解得:x=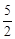 .
.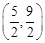 .
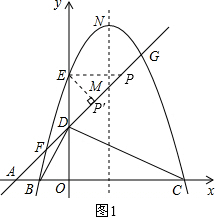
.
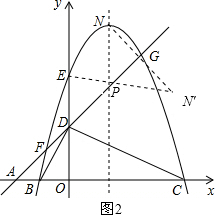
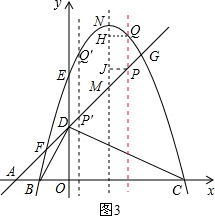


科目:初中數學 來源:不詳 題型:解答題
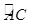 與
與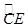 相等嗎?請證明你的結論;
相等嗎?請證明你的結論;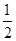 AE,是否存在過點M的直線,使該直線與(1)中所得的拋物線的兩個交點到y軸的距離相等?若存在,求出這條直線對應函數的解析式;若不存在.請說明理由.
AE,是否存在過點M的直線,使該直線與(1)中所得的拋物線的兩個交點到y軸的距離相等?若存在,求出這條直線對應函數的解析式;若不存在.請說明理由.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
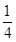 (5m2-2m+13)="0" (m為常數)的兩個實數根,點M在拋物線上,連接MQ、MH、PM,且.MP平分∠QMH,求出t值及點M的坐標.
(5m2-2m+13)="0" (m為常數)的兩個實數根,點M在拋物線上,連接MQ、MH、PM,且.MP平分∠QMH,求出t值及點M的坐標.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 銷售單價x (元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的銷售量y (件) | … | 450 | 400 | 300 | 250 | … |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
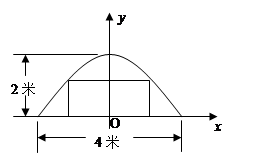
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG與□ABCD位于直線AD的同側,點F與點D重合,GF與AD在同一直線上.△EFG從點D出發以每秒1個單位的速度沿射線DA方向平移,當點G到點A時停止運動;同時點P也從點A出發,以每秒3個單位的速度沿折線AD→DC方向運動,到達點C時停止運動,設運動的時間為t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG與□ABCD位于直線AD的同側,點F與點D重合,GF與AD在同一直線上.△EFG從點D出發以每秒1個單位的速度沿射線DA方向平移,當點G到點A時停止運動;同時點P也從點A出發,以每秒3個單位的速度沿折線AD→DC方向運動,到達點C時停止運動,設運動的時間為t. 的長度;
的長度;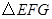 平移的過程中,記
平移的過程中,記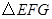 與
與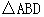 相互重疊的面積為
相互重疊的面積為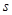 ,請直接寫出面積
,請直接寫出面積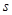 與運動時間
與運動時間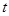 的函數關系式,并寫出
的函數關系式,并寫出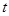 的取值范圍;
的取值范圍;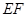 與線段
與線段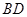 交于點
交于點 ,連接
,連接 .是否存在這樣的時間
.是否存在這樣的時間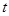 ,使得
,使得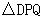 為等腰三角形?若存在,求出對應的
為等腰三角形?若存在,求出對應的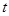 值;若不存在,請說明理由.
值;若不存在,請說明理由.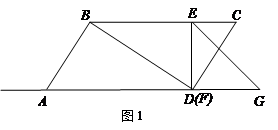
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com