
【題目】P是三角形![]() 內一點,射線PD//AC ,射線PB//AB .
內一點,射線PD//AC ,射線PB//AB .
(1)當點D,E分別在AB,BC 上時,
①補全圖1:
②猜想![]() 與
與![]() 的數量關系,并證明;,
的數量關系,并證明;,
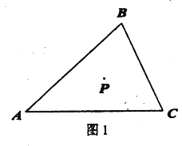
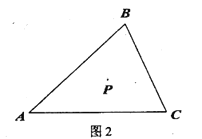
(2)當點![]() 都在線段
都在線段![]() 上時,請先畫出圖形,想一想你在(1)中所得結論是否仍然成立?若成立,請證明;若不成立,請說明理由
上時,請先畫出圖形,想一想你在(1)中所得結論是否仍然成立?若成立,請證明;若不成立,請說明理由
【答案】(1)①詳見解析;②![]() 與
與![]() 的數量關系
的數量關系![]() ;(2)不成立,此時
;(2)不成立,此時![]() ;
;
【解析】
(1)根據平行線的性質,即可得到∠A=∠BDP,∠DPE+∠BDP=180°,即可得到∠DPE與∠A的數量關系.
(2)先反向延長射線PD交AB于點D1,可知∠DPE+∠D1PE=180°,由(1)結論可知∠D1PE+∠A=180°,進而得出∠DPE=∠A.
(1)(①補全圖形,如圖1所示.
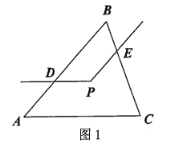
②![]() 與
與![]() 的數量關系
的數量關系![]() .
.
證明:![]() ,
,
![]()
![]() ,
,
![]() .
.
![]()
(2)不成立,此時![]()
理由如下:
如圖2,反向延長射線![]() 交
交![]() 于點
于點![]() ,
,
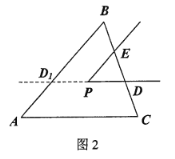
可知![]() .
.
由(1)結論可知![]()
![]()
注:用平行線的性質證明也可以.
(2)解:不成立,此時![]()
理由如下:
反向延長射線![]() 交
交![]() 于點
于點![]()
![]()
![]()
又![]()
![]()
![]()


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,點O是邊BC的中點,連接AO并延長,交DC延長線于點E,連接AC,BE.
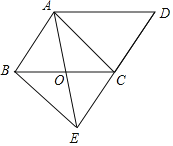
(1)求證:四邊形ABEC是平行四邊形;
(2)當∠D=50°,∠AOC=100°時,判斷四邊形ABEC的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
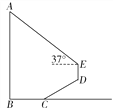
【題目】(題文)如圖,某數學活動小組為測量學校旗桿AB的高度,從旗桿正前方2![]() m處的點C出發,沿斜面坡度i=1∶
m處的點C出發,沿斜面坡度i=1∶![]() 的斜坡CD前進4m到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5 m.已知A,B,C,D,E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈
的斜坡CD前進4m到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5 m.已知A,B,C,D,E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,計算結果保留根號)
,計算結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富學生的課余生活,宣傳我縣的旅游景點,某校將舉行“我為松桃旅游代言”的活動,現隨機抽取了部分學生進行主題為“你想去的景點是 ”的問卷調查,要求學生只能去“![]() (正大苗王成),
(正大苗王成),![]() (寨英古鎮),
(寨英古鎮),![]() (盤石黔東草海),
(盤石黔東草海),![]() (烏羅潛龍洞)”四個景點選擇一項,根據調查結果,繪制了如下兩幅不完整的統計圖.回答下列問題:
(烏羅潛龍洞)”四個景點選擇一項,根據調查結果,繪制了如下兩幅不完整的統計圖.回答下列問題:

⑴本次共調查了多少名學生;
⑵請把條形統計圖補充完整;
⑶該學校共有3000名學生,試估計該校最想去盤石黔東草海的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
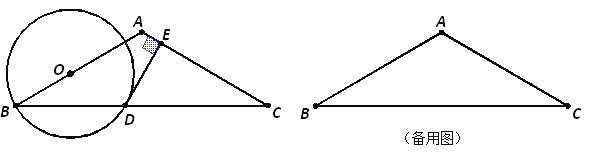
【題目】如圖,在△ABC中,AB=AC=10,∠B=30°,O是線段AB上的一個動點,以O為圓心,OB為半徑作⊙O交BC于點D,過點D作直線AC的垂線,垂足為E.
(1)求證:DE是⊙O的切線;
(2)設OB=x,求∠ODE的內部與△ABC重合部分的面積y的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩棵樹的高度分別為AB=6m,CD=8m,兩樹的根部間的距離AC=4m,小強正在距樹AB的20m的點P處從左向右前進,如果小強的眼睛與地面的距離為1.6m,當小強前進多少米時,就恰好不能看到CD的樹頂D?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() .
.

(1)如圖①,在平面直角坐標系中,以![]() 為頂點,
為頂點,![]() 為腰在第三象限作等腰
為腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 點的坐標;
點的坐標;
(2)如圖②,![]() 為
為![]() 軸負半軸上一個動點,以
軸負半軸上一個動點,以![]() 為頂點,
為頂點,![]() 為腰作等腰
為腰作等腰![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() 點,當
點,當![]() 點沿
點沿![]() 軸負半軸向下運動時,試問
軸負半軸向下運動時,試問![]() 的值是否發生變化?若不變,求其值,若變化,請說明理由;
的值是否發生變化?若不變,求其值,若變化,請說明理由;
(3)如圖③,已知點![]() 坐標為
坐標為![]() ,
,![]() 是
是![]() 軸負半軸上一點,以
軸負半軸上一點,以![]() 為直角邊作等腰
為直角邊作等腰![]() ,
,![]() 點在
點在![]() 軸上,
軸上,![]() ,設
,設![]() 、
、![]() ,當
,當![]() 點在
點在![]() 軸的負半軸上沿負方向運動時,
軸的負半軸上沿負方向運動時,![]() 的和是否發生變化?若不變,求其值;若變化,請說明理由.
的和是否發生變化?若不變,求其值;若變化,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com