
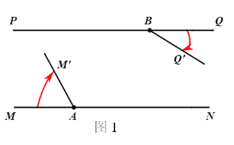
【題目】如圖1,直線MN//直線PQ,點A、B分別是直線MN、PQ上的兩點.將射線AM繞點A順時針勻速旋轉,射線BQ繞點B順時針勻速旋轉,旋轉后的射線分別記為AM′、BQ′,已知射線AM、射線BQ旋轉的速度之和為7度/秒.
(1)如果射線BQ 先轉動30°后,射線AM、BQ′再同時旋轉10秒時,射線AM′與BQ′第一次出現平行.求射線AM、BQ的旋轉速度;
(2)若射線AM、BQ分別以(1)中速度同時轉動t秒,在射線AM′與AN重合之前,求t為何值時AM′⊥BQ′;
(3)若∠BAN=45°,射線AM、BQ分別以(1)中的速度同時轉動t秒,在射線AM′與AN重合之前,射線AM′與BQ′交于點H,過點H作HC⊥PQ,垂足為C,如圖2所示,設∠BAH=α,∠BHC=β,求α和β滿足的數量關系,直接寫出結果.


【答案】(1) 射線AM、BQ的旋轉速度分別為5度/秒、2度/秒;(2) 30秒;(3) 當![]() 時,
時,![]() 45°.
45°.
【解析】(1)設射線AM、BQ的旋轉速度分別為x度/秒、y度/秒,根據速度之和等于7,以及射線AM、BQ的旋轉角度相等列方程組求解即可;
(2)根據AM′與BQ′垂直,可得![]() ,求解即可;
,求解即可;
(3)根據題意得![]() ,延長AM′與BQ交于M′,易得∠A M′B=45°-α,∠HBC=90°-β,而A M′⊥BQ′,從而求得結論.
,延長AM′與BQ交于M′,易得∠A M′B=45°-α,∠HBC=90°-β,而A M′⊥BQ′,從而求得結論.
(1)設射線AM、BQ的旋轉速度分別為x度/秒、y度/秒,根據題意得:
![]() ,解得
,解得![]()
答:射線AM、BQ的旋轉速度分別為5度/秒、2度/秒.
(2)由AM′與BQ′垂直,則![]() ,
,
![]() ,
,
答:30秒時AM′⊥BQ′
(3)易得![]() ,如圖,延長AM′與BQ交于M′,
,如圖,延長AM′與BQ交于M′,
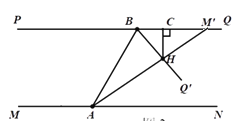
∵PQ∥MN,
∴∠AM′B=∠N AM′=45°-α,
∵HC⊥PQ,
∴∠HBC=90°-∠BHC=90°-β,
又AM′⊥BQ′,
∴∠HBC+∠AM′B=90°,
∴90°-β+45°-α=90°,即α+β=45°.


科目:初中數學 來源: 題型:
【題目】如圖,點P是正方形ABCD內一點,點P到點A、B和D的距離分別為1,2 ![]() ,
, ![]() ,△ADP沿點A旋轉至△ABP′,連結PP′,并延長AP與BC相交于點Q.
,△ADP沿點A旋轉至△ABP′,連結PP′,并延長AP與BC相交于點Q. 
(1)求證:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為提倡節約用水,準備實行自來水“階梯計費”方式,用戶用水不超出基本用水量的部分享受基本價格,超出基本用水量的部分實行加價收費,為更好地做決策,自來水公司隨機抽取部分用戶的用水量數據,并繪制了如圖不完整的統計圖(每組數據包括最大值但不包括最小值),請你根據統計圖解決下列問題:
(1)此次抽樣調查的樣本容量是
(2)補全左側統計圖,并求扇形統計圖中“25噸~30噸”部分的圓心角度數.
(3)如果自來水公司將基本用水量定為每戶25噸,那么該地區6萬用戶中約有多少用戶的用水全部享受基本價格?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題是真命題的是( )
A. 如果![]() ,則
,則 ![]()
B. 如果|a|=|b|,那么a=b
C. 兩個銳角的和是鈍角
D. 如果一點到線段兩端的距離相等,那么這點是這條線段的中點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理神秘而美妙,它的證法多樣,其巧妙各有不同,其中的“面積法”給了小聰以靈感,他驚喜的發現,當兩個全等的直角三角形如圖1或圖2擺放時,都可以用“面積法”來證明,下面是小聰利用圖1證明勾股定理的過程:
將兩個全等的直角三角形按圖1所示擺放,其中∠DAB=90°,求證:a2+b2=c2.
證明:連結DB,過點D作BC邊上的高DF,則DF=EC=b﹣a,
∵S四邊形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四邊形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
請參照上述證法,利用圖2完成下面的證明.
將兩個全等的直角三角形按圖2所示擺放,其中∠DAB=90°.求證:a2+b2=c2 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把帶有指針的圓形轉盤A、B分別分成4等份、3等份的扇形區域,并在每一個小區域內標上數字(如圖所示).小明、小樂兩個人玩轉盤游戲,游戲規則是:同時轉動兩個轉盤,當轉盤停止時,若指針所指兩區域的數字之積為3的倍數,則小明勝;否則,小樂勝.(若有指針落在分割線上,則無效,需重新轉動轉盤) 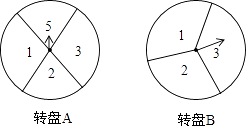
(1)試用列表或畫樹狀圖的方法,求小明獲勝的概率;
(2)請問這個游戲規則對小明、小樂雙方公平嗎?做出判斷并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,點E,F分別在邊DC,AB上,DE=BF,把平行四邊形沿直線EF折疊,使得點B,C分別落在B′,C′處,線段EC′與線段AF交于點G,連接DG,B′G.
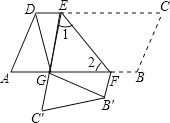
求證:(1)∠1=∠2;
(2)DG=B′G.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于頻率與概率有下列幾種說法:
①“明天下雨的概率是 90%”表示明天下雨的可能性很大;
②“拋一枚硬幣正面朝上的概率為”表示每拋兩次就有一次正面朝上;
③“某彩票中獎的概率是 1%”表示買 10 張該種彩票不可能中獎;
④“拋一枚硬幣正面朝上的概率為![]() ”表示隨著拋擲次數的增加,“拋出正面朝上”這一事件發生的頻率穩定在
”表示隨著拋擲次數的增加,“拋出正面朝上”這一事件發生的頻率穩定在![]() 附近.
附近.
正確的說法是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com