
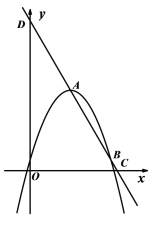
【題目】如圖所示,二次函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于A、B兩點,點B在點A的右側,直線AB分別交x軸、y軸于C、D兩點,且k<0.
的圖象交于A、B兩點,點B在點A的右側,直線AB分別交x軸、y軸于C、D兩點,且k<0.
(1)求A,B兩點橫坐標;
(2)若△OAB是以OA為腰的等腰三角形,求k的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
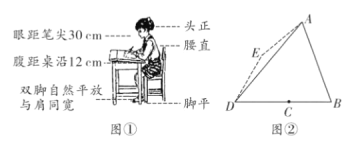
【題目】良好的坐姿習慣有利于青少年骨骼生長,有利于身體健康,那么首先要有正確的寫字坐姿,身體上半部坐直,頭部端正、目視前方,兩手放在桌面上,兩腿平放,胸膛挺起,理想狀態下,如圖①,將圖①中的眼睛記為點![]() ,腹部記為點
,腹部記為點![]() ,筆尖記為點
,筆尖記為點![]() ,且
,且![]() 與桌面沿的交點記為點
與桌面沿的交點記為點![]() ,已知
,已知![]() ,點
,點![]() 到
到![]() 的距離為23cm,
的距離為23cm, ![]() .
.
(1)求![]() 的度數
的度數
(2)老師發現小亮同學寫字姿勢不正確,眼睛傾斜到圖2的點![]() ,點
,點![]() 恰好在
恰好在![]() 的垂直平分線上,且
的垂直平分線上,且![]() ,于是要求其糾正為正確的姿勢,求眼睛所在的位置上升的距離(結果精確到1cm)
,于是要求其糾正為正確的姿勢,求眼睛所在的位置上升的距離(結果精確到1cm)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△AOB與△A1OB1是以點O為位似中心的位似圖形,且相似比為1:2,點B的坐標為(-1,2),則點B1的坐標為( )

A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
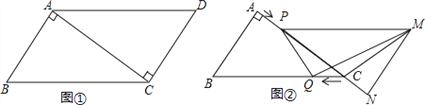
【題目】已知,如圖①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向勻速平移得到△PNM,速度為1cm/s;同時,點Q從點C出發,沿CB方向勻速移動,速度為1cm/s,當△PNM停止平移時,點Q也停止移動,如圖②,設移動時間為t(s)(0<t<4),連接PQ,MQ,MC,解答下列問題:
(1)當t為何值時,PQ∥MN?
(2)設△QMC的面積為y(cm2),求y與t之間的函數關系式;
(3)是否存在某一時刻t,使S△QMC:S四邊形ABQP=1:4?若存在,求出t的值;若不存在,請說明理由.
(4)是否存在某一時刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線交![]() 軸于
軸于![]() ,
,![]() ,交
,交![]() 軸于
軸于![]() .
.
(1)求拋物線解析式;
(2)點![]() 在第一象限的拋物線上,
在第一象限的拋物線上,![]() 與
與![]() 的面積比為
的面積比為![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,在點![]() 與
與![]() 之間的拋物線上取點
之間的拋物線上取點![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 軸于
軸于![]() 、交
、交![]() 延長線于
延長線于![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
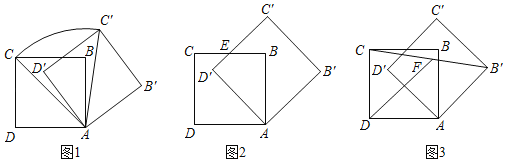
【題目】若邊長為6的正方形ABCD繞點A順時針旋轉,得正方形AB′C′D′,記旋轉角為a.
(I)如圖1,當a=60°時,求點C經過的弧![]() 的長度和線段AC掃過的扇形面積;
的長度和線段AC掃過的扇形面積;
(Ⅱ)如圖2,當a=45°時,BC與D′C′的交點為E,求線段D′E的長度;
(Ⅲ)如圖3,在旋轉過程中,若F為線段CB′的中點,求線段DF長度的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1637年笛卡兒(R.Descartes,1596-1650)在其《幾何學》中,首次應用待定系數法最早給出因式分解定理.關于笛卡爾的“待定系數法”原理,舉例說明如下:
分解因式:![]() .觀察知,顯然
.觀察知,顯然![]() 時,原式
時,原式![]() ,因此原式可分解為
,因此原式可分解為![]() 與另一個整式的積.令:
與另一個整式的積.令:![]() ,而
,而![]() ,因等式兩邊
,因等式兩邊![]() 同次冪的系數相等,則有:
同次冪的系數相等,則有: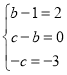 ,得
,得![]() ,從而
,從而![]()
根據以上材料,理解并運用材料提供的方法,解答以下問題:
(1)若![]() 是多項式
是多項式![]() 的因式,求
的因式,求![]() 的值并將多項式
的值并將多項式![]() 分解因式.
分解因式.
(2)若多項式![]() 含有因式
含有因式![]() 及
及![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
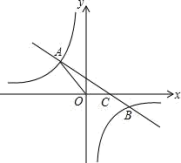
【題目】如圖,一次函數y=kx+b(k≠0)的圖象與反比例函數![]() 的圖象交于二、四象限內的A、B兩點,與x軸交于C點,點A的坐標為(﹣2,3),點B的坐標為(4,n).
的圖象交于二、四象限內的A、B兩點,與x軸交于C點,點A的坐標為(﹣2,3),點B的坐標為(4,n).
(1)求該反比例函數和一次函數的解析式;
(2)在x軸上是否存在點P,使△APC是直角三角形?若存,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com