
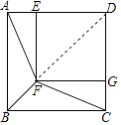
【題目】如圖,四邊形ABCD和四邊形DEFG都是正方形,點E,G分別在AD,CD上,連接AF,BF,CF 
(1)求證:AF=CF;
(2)若∠BAF=35°,求∠BFC的度數.
【答案】
(1)解:證明:∵四邊形ABCD和四邊形DEFG都是正方形,
∴AD=CD,ED=GD,FE=FG.
∴AD﹣ED=CD﹣GD.
∴AE=CG.
在△AFE和△CFG中
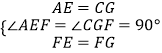 ,
,
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2)解:解:由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
連接DF,
∵四邊形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°﹣∠CFG﹣∠GFD=180°﹣35°﹣45°=100°.
即∠BFC=100°.
【解析】(1)利用正方形的性質結合全等三角形的判定與性質得出△AFE≌△CFG進而得出AF=CF;(2)利用正方形的對角線平分對角進而得出答案.
【考點精析】關于本題考查的正方形的性質,需要了解正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某通訊器材商場,計劃用40000元從廠家購進若干部新型手機,以滿足市場需求. 已知該廠家生產三種不同型號的手機,出廠價分別為:甲種型號手機每部1200元,乙種型號手機每部400元,丙種型號手機每部800元.
(1)若該商場同時購進其中兩種不同型號的手機共40部,并將40000元恰好用完. 請你幫助該商場研究一下進貨方案;
(2)商場每銷售一部甲種型號手機可獲利120元,每銷售一部乙種型號手機可獲利80元,每銷售一部丙種型號手機可獲利120元,那么在同時購進兩種不同型號手機的幾種方案中,哪種進貨方案獲利最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ABC=90°,AB=2,BC=4,現將△ABC繞頂點B順時針方向旋轉△A′BC′的位置,此時A′C′與BC的交點D是BC的中點,則線段C′D的長度是( ) 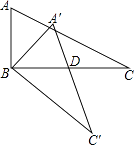
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列圖形:

它們是按一定規律排列的,依照此規律,第5個圖形中的五角星的個數為___,第n個圖形中的五角星(n為正整數)個數為____(用含n的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有20筐白菜,以每筐25千克為標準,超過或不足的千克數分別用正、負數來表示,記錄如下:
與標準質量的差值(單位:千克) |
|
|
|
|
|
|
筐 數 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最輕的一筐重______千克;
(2)與標準重量比較,20筐白菜總計超過或不足多少千克?
(3)若白菜每千克售價![]() 元,則出售這20筐白菜可賣多少元?
元,則出售這20筐白菜可賣多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,∠A=30°.

(1)用尺規作圖作AB邊上的中垂線DE,交AC于點D,交AB于點E.(保留作圖痕跡,不要求寫作法和證明);
(2)連接BD,求證:BD平分∠CBA.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A(2,0),B(0,4),作△BOC,使△BOC與△ABO全等,則點C坐標為________________________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,射線CB∥OA,∠C=∠OAB=100°,E、F在CB上,且滿足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度數;
(2)若平行移動AB,那么∠OBC∶∠OFC的值是否隨之變化?若變化,找出變化規律;若不變,求出這個比值;
(3)在平行移動AB的過程中,是否存在某種情況,使∠OEC=∠OBA?若存在,求出其度數;若不存在,說明理由。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com