
 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合). ,求y與x之間的函數(shù)解析式,并寫出函數(shù)自變量x的取值范圍.
,求y與x之間的函數(shù)解析式,并寫出函數(shù)自變量x的取值范圍. (3-x),GH=
(3-x),GH= (3-x),
(3-x), RG•GH=
RG•GH= (3-x)2,
(3-x)2, ,
, -
- (3-x)2,
(3-x)2,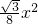 +
+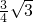 x+
x+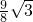 (0≤x≤3).
(0≤x≤3).

科目:初中數(shù)學(xué) 來源:第25章《圖形的變換》中考題集(17):25.2 旋轉(zhuǎn)變換(解析版) 題型:解答題
 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:第26章《圓》中考題集(08):26.1 旋轉(zhuǎn)(解析版) 題型:解答題
 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:第23章《旋轉(zhuǎn)》中考題集(06):23.1 圖形的旋轉(zhuǎn)(解析版) 題型:解答題
 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2007年全國中考數(shù)學(xué)試題匯編《圖形的平移》(02)(解析版) 題型:解答題
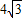 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).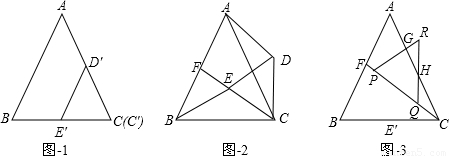
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2007年全國中考數(shù)學(xué)試題匯編《三角形》(16)(解析版) 題型:解答題
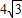 和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).
和3的兩個等邊三角形紙片ABC和C′D′E′疊放在一起(C與C′重合).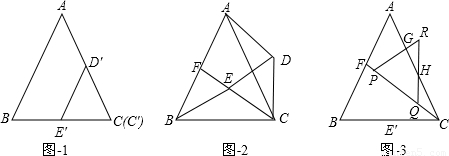
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com