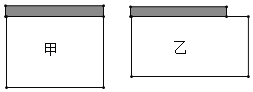
【題目】用一段長為28m的鐵絲網與一面長為8m的墻面圍成一個矩形菜園，為了使菜園面積盡可能的大，給出了甲、乙兩種圍法，請通過計算來說明這個菜園長、寬各為多少時，面積最大？最大面積是多少？
【答案】當矩形的長、寬分別為9m、9m時，面積最大，最大面積為81m2．
【解析】
根據矩形的面積公式甲圖列出算式可以直接求面積，乙圖設垂直于墻的一邊為x，則另一邊為（18﹣x）（包括墻長）列出二次函數解析式即可求解．
解：如圖甲：設矩形的面積為S，
則S＝8×
（28﹣8）＝80．
所以當菜園的長、寬分別為10m、8m時，面積為80；
如圖乙：設垂直于墻的一邊長為xm，則另一邊為（28﹣2x﹣8）+8＝（18﹣x）m．
所以S＝x（18﹣x）＝﹣x2+18x＝﹣（x﹣9）2+81
因為﹣1＜0，
當x＝9時，S有最大值為81，
所以當矩形的長、寬分別為9m、9m時，面積最大，最大面積為81m2．
綜上：當矩形的長、寬分別為9m、9m時，面積最大，最大面積為81m2．
53天天練系列答案科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，C是線段OB上的一點（不與點B重合），D，E是半圓上的點且CD與BE交于點F,用①
，②DC⊥AB，③FB=FD中的兩個作為題設，余下的一個作為結論組成一個命題，則組成真命題的個數為（ ）
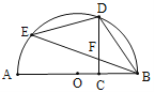
A.0B.1C.2D.3
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把分別標有數字1，2，3，4的四個小球放入A袋內，把分別標有數字－1，－2，－2，－3，5的五個小球放入B袋內，所有的小球除了標有的數字不同外，其余完全相同.
（1）學生甲從A、B兩個袋子中各摸出一個小球，求這兩個小球上的數字互為相反數的概率.
（2）當B袋中標有5的小球的數字變為 時，（1）中的概率為
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，拋物線y=a
-4ax與x軸交于A，B兩點(A在B的左側)．
(1)求點A，B的坐標；
(2)已知點C(2，1)，P(1，-
a)，點Q在直線PC上，且Q點的橫坐標為4．
①求Q點的縱坐標（用含a的式子表示）；
②若拋物線與線段PQ恰有一個公共點，結合函數圖象，求a的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
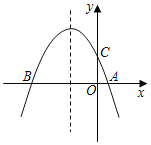
【題目】如圖，拋物線y＝﹣x2+bx+c（a≠0）與x軸交與A（1，0），B（﹣4，0）兩點．
（1）求該拋物線的解析式；
（2）設（1）中的拋物線交y軸于C點，在該拋物線的對稱軸上求出Q點的坐標使得△QAC的周長最小．
查看答案和解析>>
科目：初中數學 來源： 題型：
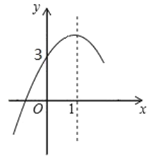
【題目】如圖，是二次函數
圖象的一部分，對稱軸是直線
，與
軸的交點是（0，3），則下列結論中正確的是（ ）
A.
；B.
>0；C.當0<
<2時，>3；D.關于的方程
有兩個相等的實數根
查看答案和解析>>
科目：初中數學 來源： 題型：
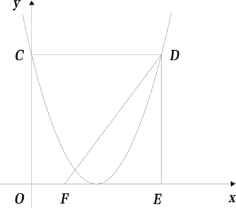
【題目】已知二次函數
的圖象與
軸交于點C，過點C作CD∥
軸交該函數的圖象于點D，過點D作DE∥軸交軸于點E，已知點F（1，0），連接DF.
（1）請求出該函數圖象的項點坐標（用含
的代數式表示）；
（2）如圖，若該二次函數的圖象的頂點落在軸上，P為對稱軸右側拋物線上一點；
①連接PD、PE、PF，若
，求點P的坐標；
②若∠PFD=
∠DEF，點P的橫坐標為m，則m的值為 .
查看答案和解析>>
科目：初中數學 來源： 題型：
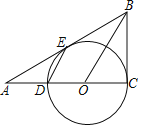
【題目】如圖，點D、O在△ABC的邊AC上，以CD為直徑的⊙O與邊AB相切于點E，連結DE、OB，且DE∥OB．
（1）求證：BC是⊙O的切線．
（2）設OB與⊙O交于點F，連結EF，若AD＝OD，DE＝4，求弦EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
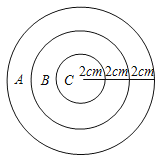
【題目】如圖為一個封閉的圓形裝置，整個裝置內部為A、B、C三個區域（A、B兩區域為圓環，C區域為小圓），具體數據如圖．
（1）求出A、B、C三個區域三個區域的面積：SA＝ ，SB＝ ，SC＝ ；
（2）隨機往裝置內扔一粒豆子，多次重復試驗，豆子落在B區域的概率PB為多少？
（3）隨機往裝置內扔180粒豆子，請問大約有多少粒豆子落在A區域？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com