
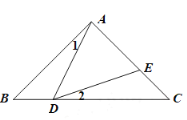
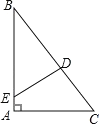
【題目】如圖,在等腰三角形ABC中,∠BAC=90°,AB=AC=2,D是BC邊上的一個動點,(不與B、C重合)在AC邊上取一點E,使∠ADE=45°.
(1)求證:△ABD∽△DCE;
(2)設BD=x,AE=y.
①求y關于x的函數關系式并寫出自變量x的取值范圍;
②求y的最小值.

【答案】(1)見解析;(2)①![]() ,②1
,②1
【解析】
(1)根據等腰直角三角形的性質得到∠B=∠C=45°,根據三角形的外角性質得到∠BAD=∠EDC,根據相似三角形的判定定理證明結論;
(2)①根據相似三角形的性質列出比例式,代入計算得到y關于x的函數關系式;
②根據二次函數的性質計算即可.
(1)證明:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠1=45°+∠1,∠ADC=∠ADE+∠2=45°+∠2,
∴∠1=∠2.
∴△ABD∽△DCE.
(2)解:①∵△ABD∽△DCE,
∴![]() .
.
∵AB=AC=2,BD=x,AE=y,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
② ∵![]() ,
,
∴y的最小值是1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
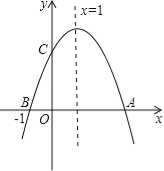
【題目】如圖,二次函數![]() (a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,且對稱軸為x=1,點B坐標為(﹣1,0).則下面的四個結論:①2a+b=0;②4a-2b+c<0;③ac>0;④當y<0時,x<-1或x>2.其中正確的個數是
(a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,且對稱軸為x=1,點B坐標為(﹣1,0).則下面的四個結論:①2a+b=0;②4a-2b+c<0;③ac>0;④當y<0時,x<-1或x>2.其中正確的個數是
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
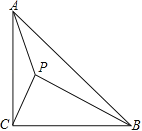
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,P是△ABC形內一點,且∠APB=∠APC=135°.
(1)求證:△CPA∽△APB;
(2)試求tan∠PCB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月12日華為新出的型號為“P30 Pro”的手機在上海召開發布會,某華為手機專賣網店抓住商機,購進10000臺“P30 Pro”手機進行銷售,每臺的成本是4400元,在線同時向國內、國外發售.第一個星期,國內銷售每臺售價是5400元,共獲利100萬元,國外銷售也售出相同數量該款手機,但每臺成本增加400元,獲得的利潤卻是國內的6倍.
(1)求該店銷售該款華為手機第一個星期在國外的售價是多少元?
(2)受中美貿易戰影響,第二個星期,國內銷售每臺該款手機售價在第一個星期的基礎上降低m%,銷量上漲5m%;國外銷售每臺售價在第一個星期的基礎上上漲m%,并且在第二個星期將剩下的手機全部賣完,結果第二個星期國外的銷售總額比國內的銷售總額多6993萬元,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
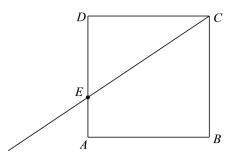
【題目】已知:如圖,在正方形ABCD中,點E在AD邊上運動,從點A出發向點D運動,到達D點停止運動.作射線CE,并將射線CE繞著點C逆時針旋轉45°,旋轉后的射線與AB邊交于點F,連接EF
(1)依題意補全圖形;
(2)猜想線段DE,EF,BF的數量關系并證明;
(3)過點C作CG⊥EF,垂足為點G,若正方形ABCD的邊長是4,請直接寫出點G運動的路線長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C為⊙O上一點,AE和過點C的切線互相垂直,垂足為E,AE交⊙O于點D,直線EC交AB的延長線于點P,連接AC,BC,PB:PC=1:2.

(1)求證:AC平分∠BAD;
(2)探究線段PB,AB之間的數量關系,并說明理由;
(3)若AD=3,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在某次斯諾克比賽中,白球位于點 A 處,在點 A 正北方向的點 B 處有一顆紅球,在點 A 正東方向 C 處有一顆黑球,在 BC 正中間的點 D 處有一顆籃球,其中點 C 在點 B 的南偏東 37°方向上,選手將白球沿正北方想推進 10cm 到達點 E 處時,測得點D 在點E 的北偏東45°方向上,求此時白球與紅球的距離有多遠?(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,BC=8cm,射線AG∥BC,點E從點A出發沿射線AG以1cm/s的速度運動,同時點F從點B出發沿射線BC以2cm/s的速度運動,設運動時間為t(s).
(1)連接EF,當EF經過AC邊的中點D時,求證:△ADE≌△CDF;
(2)①當t為 時,以A、F、C、E為頂點的四邊形是平行四邊形(直接寫出結果);
②當t為 時,四邊形ACFE是菱形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com