Question

如圖1所示，在△ABC中，∠BAC=90°，AB=AC，AE是過A的一條直線，且B、C在AE的異側，BD⊥AE于D，CE⊥AE于E．求證：
（1）BD=DE+CE．
（2）若直線AE繞A點旋轉到如圖2位置時（BD＜CE），其他條件不變，判斷BD與DE，CE的關系并說明理由．
（3）若直線AE繞A點旋轉到如圖3位置時（BD＞CE），其他條件不變，則BD與DE，CE的關系又怎樣？請寫出結果，不必證明．

Answer 1

解：證明如下：
（1）∵∠BAC=90°，∴∠BAD+∠CAE=90°，
∵CE⊥AE，∴∠ACE+∠CAE=90°，
∴∠ACE=∠BAD；
又∵BD⊥AE，CE⊥AE，
∴∠ADB=∠CEA=90°，
在△ABD和△CAE中，
，
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE；
∵AE=DE+AD，
∴BD=DE+CE；

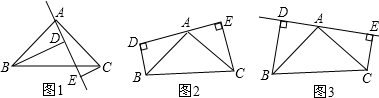
（2）DE=BD+CE．
∵∠BAC=90°，∴∠BAD+∠CAE=90°，
∵CE⊥AE，∴∠ACE+∠CAE=90°，
∴∠ACE=∠BAD；
又∵BD⊥AE，CE⊥AE
∴∠ADB=∠CEA=90°，
在△ABD和△CAE中，
，
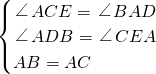
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE；
∵DE=AE+AD，
∴DE=BD+CE；

（3）結論是：當B、C在AE兩側時，BD=DE+CE；當B、C在AE同側時，BD=DE-CEDE=BD+CE．
分析：（1）根據已知條件易證得∠BAD=∠ACE，且根據全等三角形的判定可證明△ABD≌△CAE，根據各線段的關系即可得結論．
（2）BD=DE+CE．根據全等三角形的判定可證明△ABD≌△CAE，根據各線段的關系即可得結論．
（3）同上理，BD=DE+CE仍成立．
點評：本題考查了全等三角形的判定和性質，涉及到直角三角形的性質、余角和補角的性質等知識點，熟練掌握全等三角形的判定方法是解題的關鍵．
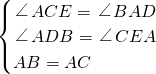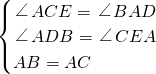