
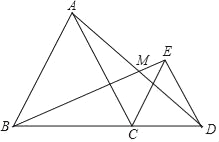
【題目】如圖,B、C、D在同一直線上,△ABC和△ECD都是等邊三角形,BE與AD相交于點M,
(1)求證:∠CBE=∠CAD;
(2)由(1)可知,圖中的△EBC是由△DAC怎樣變換(填一種變換)得到的.
【答案】(1)見解析;(2)逆時針旋轉60°
【解析】
(1)由等邊三角形的性質可得出AC=BC、CD=CE、∠BCA=∠DCE=60°,進而可得出∠BCE=∠ACD,利用全等三角形的判定定理SAS可證出△ACD≌△BCE,再根據全等三角形的性質可證出∠CBE=∠CAD;
(2)由B、C、D在同一直線上結合∠BCA=∠DCE=60°,可求出∠ACE=60°,由△ACD≌△BCE結合圖形,可得出圖中的△EBC是由△DAC逆時針旋轉60°得到的.
(1)證明:∵△ABC和△ECD都是等邊三角形,
∴AC=BC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD.
在△ACD和△BCE中,

∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD.
(2)∵B、C、D在同一直線上,∠BCA=∠DCE=60°,
∴∠ACE=60°.
∵△ACD≌△BCE,
∴圖中的△EBC是由△DAC逆時針旋轉60°得到的.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
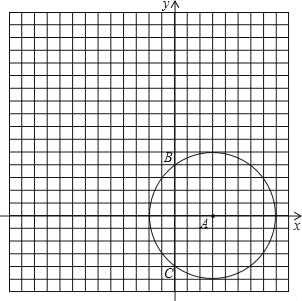
【題目】如圖,正方形網格中,每個小正方形的邊長為1個單位,以O為原點建立平面直角坐標系,圓心為 A(3,0)的⊙A被y軸截得的弦長BC=8.
解答下列問題:
(1)求⊙A 的半徑;
(2)請在圖中將⊙A 先向上平移 6 個單位,再向左平移8個單位得到⊙D,并寫出圓心D的坐標;
(3)觀察你所畫的圖形,對⊙D 與⊙A 的位置關系作出合情的猜想,并直接寫出你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD內有兩點E、F滿足AE=FC= 4,EF =6,AE⊥EF,CF⊥EF,則正方形ABCD的面積為 ( )
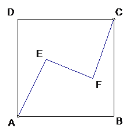
A.24B.25C.48D.50
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了處理污水需要鋪設一條長為2000米的管道,實際施工時,×××××××,設原計劃每天鋪設管道![]() 米,則可列方程
米,則可列方程![]() ,根據此情景,題目中的“×××××××”表示所丟失的條件,這一條件為( )
,根據此情景,題目中的“×××××××”表示所丟失的條件,這一條件為( )
A.每天比原計劃多鋪設10米,結果延期10天完成任務
B.每天比原計劃少鋪設10米,結果延期10天完成任務
C.每天比原計劃少鋪設10米,結果提前10天完成任務
D.每天比原計劃多鋪設10米,結果提前10天完成任務
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,A(﹣3,0),B(0,4),對△AOB按圖示方式連續作旋轉變換,這樣算到的第2016個三角形時,A點的對應點的坐標為( )
A. (8064,4) B. (8064,0) C. (8064,3) D. (8061,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:關于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求證:無論m取何值時,方程恒有實數根;
(2)若關于x的二次函數y=mx2﹣(3m﹣1)x+2m﹣2的圖象與x軸兩交點間的距離為2時,求拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
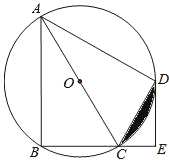
【題目】如圖,四邊形ABCD是⊙O的內接四邊形,![]() ,AC為直徑,DE⊥BC,垂足為E.
,AC為直徑,DE⊥BC,垂足為E.
(1)求證:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
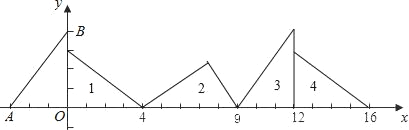
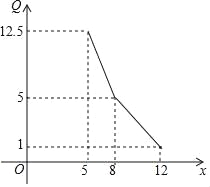
【題目】某專賣店經市場調查得知,一種商品的月銷售量 Q(單位:噸)與銷售價格 x(單位:萬元/噸)的關系可用下圖中的折線表示.
(1)寫出月銷售量 Q 關于銷售價格 x 的關系;
(2)如果該商品的進價為 5 萬元/噸,除去進貨成本外,專賣店銷售該商品每月的固定成本為 10 萬元,問該商品 每噸定價多少萬元時,銷售該商品的月利潤最大?并求月利潤的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com