已知方程2(m+1)x2+4mx+3m=2,根據下列條件之一求m的值.
(1)方程有兩個相等的實數根;
(2)方程有兩個相反的實數根;
(3)方程的一個根為0.
【答案】
分析:(1)根據△=0,得出關于m的方程求出m的值;
(2)方程兩實數根相反即兩根和=0,根據根與系數的關系得出關于m的方程求出m的值并檢驗;
(3)把X=0代入原方即可求出m的值.
解答:解:(1)∵△=16m
2-8(m+1)(3m-2)=-8m
2-8m+16,
而方程有兩個相等的實數根,
∴△=0,即-8m
2-8m+16=0,
求得m
1=-2,m
2=1;
(2)因為方程有兩個相等的實數根,
所以兩根之和為0且△≥0,則-
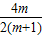
=0,
求得m=0;
(3)∵方程有一根為0,
∴3m-2=0,
∴m=

.
點評:此題考查了的判別式,根與系數的關系,代入法求方程的解,綜合性比較強.
