
推理證明:如圖,已知△ABC中,AB=BC,以AB為直徑的⊙O交AC于點D過D作DE⊥BC,垂足為E,連結OE,CD=![]() ,∠ACB=30°.
,∠ACB=30°.
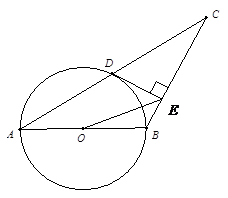
(1)求證:DE是⊙O的切線;
(2)分別求AB,OE的長;
(3)填空:如果以點E為圓心,r為半徑的圓上總存在不同的兩點到點O的距離為1,則r的取值范圍為 .
(1)見解析(2)2,![]() (3)
(3)![]()
解析:(1)證明:連接BD 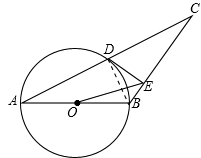
∵AB是直徑,
∴∠ADB=90°
又∵AB=BC,
∴AD=CD,
∴OD∥BC
∴OD⊥DE,
∴DE是⊙O的切線.(4分)
(2)解:在Rt△CBD中CD= ![]() ,∠ACB=30°,
,∠ACB=30°,
∴BC=CD8 cos30° = ![]() =2,
=2,
∴AB=2.
在Rt△CDE中,CD=![]() ,∠ACB=30°,
,∠ACB=30°,
∴DE=![]() CD=
CD=![]() ×
×![]() =
= ![]() .
.
在Rt△ODE中,OE=![]() =
=![]()
(3)![]() ………9分
………9分
(1)根據AB是直徑即可求得∠ADB,再根據題意可求出OD⊥DE,即得出結論;
(2)根據三角函數的定義,即可求得AB,再在Rt△CDE中,根據直角三角形的性質,可求得DE,再由勾股定理求出OE即可
(3)根據兩圓的位置關系解答


科目:初中數學 來源: 題型:
 完成下列推理過程:
完成下列推理過程:查看答案和解析>>
科目:初中數學 來源: 題型:
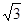 ,∠ACB=30°.
,∠ACB=30°.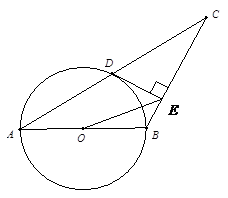
查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省南通一中九年級中考適應性考試(三)數學卷(帶解析) 題型:解答題
推理證明:如圖,已知△ABC中,AB=BC,以AB為直徑的⊙O交AC于點D過D作DE⊥BC,垂足為E,連結OE,CD=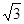 ,∠ACB=30°.
,∠ACB=30°.
(1)求證:DE是⊙O的切線;
(2)分別求AB,OE的長;
(3)填空:如果以點E為圓心,r為半徑的圓上總存在不同的兩點到點O的距離為1,則r的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省九年級中考適應性考試(三)數學卷(解析版) 題型:解答題
推理證明:如圖,已知△ABC中,AB=BC,以AB為直徑的⊙O交AC于點D過D作DE⊥BC,垂足為E,連結OE,CD=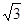 ,∠ACB=30°.
,∠ACB=30°.
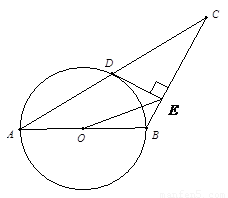
(1)求證:DE是⊙O的切線;
(2)分別求AB,OE的長;
(3)填空:如果以點E為圓心,r為半徑的圓上總存在不同的兩點到點O的距離為1,則r的取值范圍為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com