
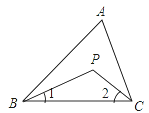
【題目】如圖所示,在△ABC中,BP、CP分別是∠ABC和∠ACB的角平分線,∠BPC=134°,求∠A的度數.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知BD,CE是△ABC的兩條高,直線BD,CE相交于點H.

(1)若∠BAC=100°,求∠DHE的度數;
(2)若△ABC中∠BAC=50°,直接寫出∠DHE的度數是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,P是AD上一動點,O為BD的中點,連接PO并延長,交BC于點Q.
(1) 求證:四邊形PBQD是平行四邊形
(2) 若AD=6cm,AB=4cm, 點P從點A出發,以1cm/s的速度向點D運動(不與點D重合),設點P運動時間為t s , 請用含t的代數式表示PD的長,并求出當t為何值時,四邊形PBQD是菱形。并求出此時菱形的周長。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 過點(2,-1),與
過點(2,-1),與![]() 軸交于點A,F點為(1,2).
軸交于點A,F點為(1,2).
(Ⅰ)求![]() 的值及A點的坐標;
的值及A點的坐標;
(Ⅱ)將函數![]() 的圖象沿
的圖象沿![]() 軸方向向上平移得到函數
軸方向向上平移得到函數![]() ,其圖象與
,其圖象與![]() 軸交于點Q,且OQ=QF,求平移后的函數
軸交于點Q,且OQ=QF,求平移后的函數![]() 的解析式;
的解析式;
(Ⅲ)若點A關于![]() 的對稱點為K,請求出直線FK與
的對稱點為K,請求出直線FK與![]() 軸的交點坐標.
軸的交點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:平面內點A到圖形G上各個點的距離的最小值稱為該點到這個圖形的最小距離d,點A到圖形G上各個點的距離的最大值稱為該點到這個圖形的最大距離D,定義點A到圖形G的距離跨度為R=D﹣d. 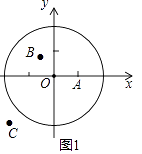
(1)①如圖1,在平面直角坐標系xOy中,圖形G1為以O為圓心,2為半徑的圓,直接寫出以下各點到圖形G1的距離跨度: A(1,0)的距離跨度;
B(﹣ ![]() ,
, ![]() )的距離跨度;
)的距離跨度;
C(﹣3,﹣2)的距離跨度;
②根據①中的結果,猜想到圖形G1的距離跨度為2的所有的點組成的圖形的形狀是 .
(2)如圖2,在平面直角坐標系xOy中,圖形G2為以D(﹣1,0)為圓心,2為半徑的圓,直線y=k(x﹣1)上存在到G2的距離跨度為2的點,求k的取值范圍. 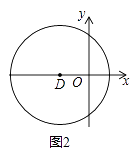
(3)如圖3,在平面直角坐標系xOy中,射線OP:y= ![]() x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,直接寫出圓心E的橫坐標xE的取值范圍 .
x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,直接寫出圓心E的橫坐標xE的取值范圍 . 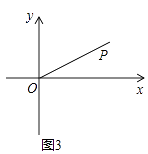
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l:![]() ,過點M(1,0)作x軸的垂線交直線l于點N,過點N作直線l的垂線交x軸于點M1;過點M1作x軸的垂線交直線l于N1,過點N1作直線l的垂線交x軸于點M2,…;按此作法繼續下去,則點M5的坐標為_____.
,過點M(1,0)作x軸的垂線交直線l于點N,過點N作直線l的垂線交x軸于點M1;過點M1作x軸的垂線交直線l于N1,過點N1作直線l的垂線交x軸于點M2,…;按此作法繼續下去,則點M5的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解家長關注孩子成長方面的狀況,學校開展了針對學生家長的“您最關心孩子哪方面成長”的主題調查,調查設置了“健康安全”、“日常學習”、“習慣養成”、“情感品質”四個項目,并隨機抽取甲、乙兩班共100位學生家長進行調查,根據調查結果,繪制了如圖不完整的條形統計圖. 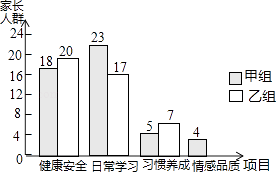
(1)補全條形統計圖.
(2)若全校共有3600位學生家長,據此估計,有多少位家長最關心孩子“情感品質”方面的成長?
(3)綜合以上主題調查結果,結合自身現狀,你更希望得到以上四個項目中哪方面的關注和指導?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,需在一面墻上繪制幾個相同的拋物線型圖案.按照圖中的直角坐標系,最左邊的拋物線可以用y=ax2+bx(a≠0)表示.已知拋物線上B,C兩點到地面的距離均為 ![]() m,到墻邊OA的距離分別為
m,到墻邊OA的距離分別為 ![]() m,
m, ![]() m.
m. 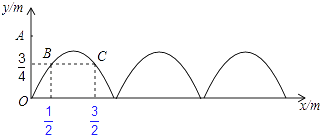
(1)求該拋物線的函數關系式,并求圖案最高點到地面的距離;
(2)若該墻的長度為10m,則最多可以連續繪制幾個這樣的拋物線型圖案?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com