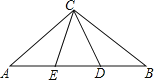
【題目】如圖，△ABC中，AC＝AD，BC＝BE，∠ACB＝100°，則∠ECD＝（ ）
A.20°B.30°C.40°D.50°
【答案】C
【解析】
首先設∠ACE=x°，∠DCE=y°，∠BCD=z°，由BE=BC，AD=AC，利用等腰三角形的性質，即可用x，y，z表示出∠ADC與∠BEC的度數，又由三角形外角的性質，得到∠A與∠B的值，然后由在△ABC中，∠ACB=100°，利用三角形內角和定理得到方程，繼而求得∠DCE的大小．
設∠ACE＝x°，∠DCE＝y°，∠BCD＝z°，
∵BE＝BC，AD＝AC，
∴∠ADC＝∠ACD＝∠ACE+∠DCE＝（x+y）°，∠BEC＝∠BCE＝∠BCD+∠DCE＝（y+z）°，
∴∠A＝∠BEC﹣∠ACE＝（y+z﹣x）°，∠B＝∠ADC﹣∠BCD＝（x+y﹣z）°，
∵在△ABC中，∠ACB＝100°，
∴∠A+∠B＝180°﹣∠ACB＝80°，
∴y+z﹣x+x+y﹣z＝80，
即2y＝80，
∴y＝40，
∴∠DCE＝40°．
故選C．
科目：初中數學 來源： 題型：
【題目】
如圖
，
中，
平分
交
于點
，在
上截取
，過點
作
交于點
．求證：四邊形
是菱形；
如圖
，中，平分的外角
交的延長線于點，在
的延長線上截取，過點作交
的延長線于點．四邊形還是菱形嗎？如果是，請證明；如果不是，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，菱形
的面積為
，對角線
，
交于點
，點
，
，
，
分別是
，
，
，
的中點，連接
，
，
，
得到菱形
；點
，
，
，
分別是
，
，
，
的中點，連接
，
，
，
，得到菱形
；…，依此類推，則菱形
的面積為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分別為E，F．
（1）求證：△ABE≌△CDF；
（2）若AC與BD交于點O，求證：AO=CO．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是過A的一條直線, 且B、C在AE的異側, BD⊥AE于D, CE⊥AE于E.
(1)求證: BD=DE+CE.
(2)若直線AE繞A點旋轉到圖②位置時(BD<CE), 其余條件不變, 問BD與DE、CE的數量關系如何? 請給予證明；
(3)若直線AE繞A點旋轉到圖③位置時(BD>CE), 其余條件不變, 問BD與DE、CE的數量關系如何? 請直接寫出結果, 不需證明.
(4)根據以上的討論，請用簡潔的語言表達BD與DE,CE的數量關系。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．
（1）求證：△ADC≌△CEB．
（2）AD=5cm，DE=3cm，求BE的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，⊙O是△ABC的外接圓，AB為直徑，∠BAC的平分線交⊙O于點D，過點D的切線分別交AB，AC的延長線于點E，F．
（1）求證：AF⊥EF．
（2）探究線段AF、CF、AB之間的數量關系，并證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在平面直角坐標系中有
，
兩點，現從
、
、
、
四點中，任選兩點作為
、
，則以
、
、、四個點為頂點所組成的四邊形中是平行四邊形的概率是________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明為校合唱隊購買某種服裝時，商店經理給出了如下優惠條件：如果一次性購買不超過
件，單價為
元；如果一次性購買多于件，那么每增加
件，購買的所有服裝的單價降低
元，但單價不得低于
元．按此優惠條件，小明一次性購買這種服裝
（為正整數）件，支付
元．
當
時，小明購買的這種服裝的單價為________元；
寫出關于的函數表達式，并給出自變量的取值范圍；
小明一次性購買這種服裝付了
元，請問他購買了多少件這種服裝？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com