解:(1)∵在△ABM和△BCN中,

,
∴△ABM≌△BCN(SAS).
∴∠BAM=∠CBN(全等三角形對應角相等).
∵∠QBA+∠CBN=∠CBA=60°(已知),
∴∠QBA+∠BAM=60°(等量代換).
∴∠BQM=60°.
(2)①是.
∵∠BQM=60°(已知),
∴∠QBA+∠BAM=60°.
∵∠QBA+∠CBN=60°(由(1)得出的結論),
∴∠BAM=∠CBN(等量代換).
在△ABM和△BCN中,

∴△ABM≌△BCN(ASA).
∴BM=CN(全等三角形對應邊相等).
②成立.
∵BM=CN(①的結論),
∴CM=AN(等量代換).
∵AB=AC,∠ACM=∠BAN=180°-60°=120°(平角的性質),
在△BAN和△ACM中,

∴△BAN≌△ACM(SAS).
∴∠NBA=∠MAC,
∴∠BQM=∠BNA+∠NAQ=180°-∠NCB-(∠CBN-∠NAQ)=180°-60°-60°=60°(三角形內角和定理).
分析:(1)由已知條件得△ABM≌△BCN,得∠BAM=∠CBN,又因為∠QBA+∠CBN=∠CBA=60°,所以∠QBA+∠BAM=60°,即有∠BQM=60°;
(2)①因為∠BQM=60°,所以∠QBA+∠BAM=60°,又因為∠QBA+∠CBN=60°,所以∠BAM=∠CBN,已知∠B=∠C,AB=AC,則ASA可判定△ABM≌△BCN,即BM=CN;②成立.
點評:本題考查了全等三角形的判定和性質及等邊三角形的性質;此題把全等三角形的判定和性質結合求解.有利于培養學生綜合運用數學知識的能力,全等三角形的證明是正確解答本題的關鍵.

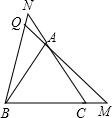
 =CN,AM、BN交于點Q,求證:∠BQM=60°.
=CN,AM、BN交于點Q,求證:∠BQM=60°. ,
, (2)①是.
(2)①是.



 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案 =CN,AM、BN交于點Q,求證:∠BQM=60°.
=CN,AM、BN交于點Q,求證:∠BQM=60°.