
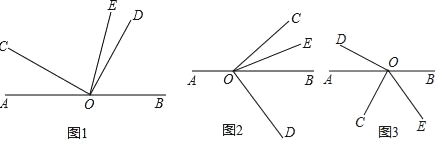
【題目】已知直線AB經過點O,∠COD=90°,OE是∠BOC的平分線.
(1)如圖1,若∠AOC=50°,求∠DOE;
(2)如圖1,若∠AOC=α,求∠DOE;(用含α的式子表示)
(3)將圖1中的∠COD繞頂點O順時針旋轉到圖2的位置,其它條件不變,(2)中的結論是否還成立?試說明理由;
(4)將圖1中的∠COD繞頂點O逆時針旋轉到圖3的位置,其它條件不變,求∠DOE.(用含α的式子表示)
【答案】(1)25°;(2)![]() ;(3)(2)中的
;(3)(2)中的![]() 結論還成立,理由見解析;(4)180°﹣
結論還成立,理由見解析;(4)180°﹣![]() .
.
【解析】
(1)如圖1,根據平角的定義和∠COD=90°,得∠AOC+∠BOD=90°,從而求得:∠BOD=40°,由角平分線定義得:∠BOE=![]() ∠BOC=65°,利用角的差可得結論;
∠BOC=65°,利用角的差可得結論;
(2)同理可得:∠DOE=![]() α;
α;
(3)如圖2,根據平角的定義得:∠BOC=180°-α,由角平分線定義得:∠EOC=![]() ∠BOC=90°-
∠BOC=90°-![]() α,根據角的差可得(2)中的結論還成立;
α,根據角的差可得(2)中的結論還成立;
(4)同理可得:∠DOE=∠COD+∠COE=180°-![]() α.
α.
解:(1)如圖1,∵∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=50°,
∴∠BOD=40°,
∴∠BOC=∠COD+∠BOD=90°+40°=130°,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=65°,
∠BOC=65°,
∴∠DOE=65°﹣40°=25°;
(2)如圖1,由(1)知:∠AOC+∠BOD=90°,
∵∠AOC=α,
∴∠BOD=90°﹣α,
∴∠BOC=∠COD+∠BOD=90°+90°﹣α=180°﹣α,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC =90﹣
∠BOC =90﹣![]() α,
α,
∴∠DOE=∠BOE﹣∠BOD=90°﹣![]() α﹣(90°﹣α)=
α﹣(90°﹣α)=![]() α,
α,
(3),(2)中的結論還成立,理由是:
如圖2,∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°﹣α,
∵OE平分∠BOC,
∴∠EOC=![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() α,
α,
∵∠COD=90°,
∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣![]() α)=
α)=![]() α;
α;
(4)如圖3,∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°﹣α,
∵OE平分∠BOC,
∴∠EOC=![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() α,
α,
∵∠COD=90°,
∴∠DOE=∠COD+∠COE=90°+(90°﹣![]() α)=180°﹣
α)=180°﹣![]() α.
α.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在求1+3+32+33+34+35+36+37+38的值時,張紅發現:從第二個加數起每一個加數都是前一個加數的3倍,于是她假設:S=1+3+32+33+34+35+36+37+38①, 然后在①式的兩邊都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= ![]() .
.
得出答案后,愛動腦筋的張紅想:如果把“3”換成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正確答案是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC、BDEF是面積分別為![]() 、
、![]() 的正方形,點A在x軸上,點F在BC上,點E在反比例函數
的正方形,點A在x軸上,點F在BC上,點E在反比例函數![]() (k>0)的圖象上,若
(k>0)的圖象上,若![]() ,則k值為( )
,則k值為( )

A. 1 B. ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:如圖(1),點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,試判斷BE、EF、FD之間的數量關系.
(1)【發現證明】
小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖(1)證明上述結論.
(2)【類比引申】
如圖(2),四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足關系時,仍有EF=BE+FD.
(3)【探究應用】
如圖(3),在某公園的同一水平面上,四條通道圍成四邊形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分別有景點E、F,且AE⊥AD,DF=40( ![]() ﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長(結果取整數,參考數據:
﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長(結果取整數,參考數據: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,拋物線經過點A(0,4),B(1,0),C(5,0),其對稱軸與x軸相交于點M.
(1)求拋物線的解析式和對稱軸;
(2)在拋物線的對稱軸上是否存在一點P,使△PAB的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)連接AC,在直線AC的下方的拋物線上,是否存在一點N,使△NAC的面積最大?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)△ABC在平面直角坐標系中的位置如圖所示,其中每個小正方形的邊長為1個單位長度.
(1)按要求作圖:
①畫出△ABC關于原點O的中心對稱圖形△A1B1C1;
②畫出將△ABC繞點A逆時針旋轉90°得到△AB2C2,
(2)回答下列問題:
①△A1B1C1中頂點A1坐標為 ;②若P(a,b)為△ABC邊上一點,則按照(1)中①作圖,點P對應的點P1的坐標為 .

【答案】(1)作圖見解析;(2)(1,-2)(-a,-b)
【解析】試題分析:(1)首先找出對應點的位置,再順次連接即可;
(2)①根據圖形可直接寫出坐標;②根據關于原點對稱點的坐標特點可得答案.
試題解析:(1)如圖所示:
(2)①根據圖形可得A1坐標為(2,﹣4);
②點P1的坐標為(﹣a,﹣b).
故答案為:(﹣2,﹣4);(﹣a,﹣b).

考點:作圖-旋轉變換.
【題型】填空題
【結束】
23
【題目】在學習了“普查與抽樣調查”之后,某校八(1)班數學興趣小組對該校學生的視力情況進行了抽樣調查,并畫出了如圖所示的條形統計圖.請根據圖中信息解決下列問題:
(1)本次抽查活動中共抽查了 名學生;
(2)已知該校七年級、八年級、九年級學生數分別為360人、400人、540人.
①試估算:該校九年級視力不低于4.8的學生約有 名;
②請你幫忙估算出該校視力低于4.8的學生數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,∠B=90°,以AB上的一點O為圓心,以OA為半徑的圓交AC于點D,交AB于點E. 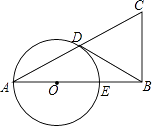
(1)求證:ACAD=ABAE;
(2)如果BD是⊙O的切線,D是切點,E是OB的中點,當BC=2時,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生的課外閱讀情況,就“我最喜愛的課外讀物”對文學、藝術、科普和其他四個類別進行了抽樣調查(每位同學只選一類),并根據調查結果繪制了兩幅不完整的統計圖,請你根據圖中提供的信息,解答下列問題: 
(1)這次被調查的學生共有多少名?
(2)請將條形統計圖補充完整;并在扇形統計圖中,計算出“其他類”所對應的圓心角的度數;
(3)若該校有2400名學生,請你估計該校喜愛“科普類”的學生有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在數軸l上,一動點Q從原點O出發,沿直線l以每秒鐘2個單位長度的速度來回移動,其移動方式是先向右移動1個單位長度,再向左移動2個單位長度,又向右移動3個單位長度,再向左移動4個單位長度,又向右移動5個單位長度…
![]()
(1)求出5秒鐘后動點Q所處的位置;
(2)如果在數軸l上還有一個定點A,且A與原點O相距20個單位長度,問:動點Q從原點出發,可能與點A重合嗎?若能,則第一次與點A重合需多長時間?若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com