
【題目】如圖,在平面直角坐標系![]() 中,二次函數
中,二次函數![]() 的圖象經過點
的圖象經過點![]() ,且當
,且當![]() 和
和![]() 時所對應的函數值相等.一次函數
時所對應的函數值相等.一次函數![]() 與二次函數
與二次函數![]() 的圖象分別交于
的圖象分別交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在第一象限.
在第一象限.

(![]() )求二次函數
)求二次函數![]() 的表達式.
的表達式.
(![]() )連接
)連接![]() ,求
,求![]() 的長.
的長.
(![]() )連接
)連接![]() ,
, ![]() 是線段
是線段![]() 得中點,將點
得中點,將點![]() 繞點
繞點![]() 旋轉
旋轉![]() 得到點
得到點![]() ,連接
,連接![]() ,
, ![]() ,判斷四邊形
,判斷四邊形![]() 的性狀,并證明你的結論.
的性狀,并證明你的結論.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析
;(3)見解析
【解析】(1)根據當x=0和x=5時所對應的函數值相等,可得(5,c),根據待定系數法,可得函數解析式;
(2)聯立拋物線與直線,可得方程組,根據解方程組,可得B、C 的坐標根據勾股定理,可得AB的長;
(3)根據線段中點的性質,可得M點的坐標,根據旋轉的性質,可得MN與BM的關系,根據平行四邊形的判定,可得答案.
解:(![]() )當
)當![]() 時
時![]() .即
.即![]() .
.
把![]()
![]() 代入解析式.
代入解析式.
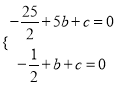 ,∴
,∴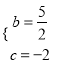 ,
,
∴![]() .
.
(![]() )∵
)∵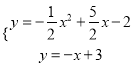 ,∴
,∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴![]() .
.
(![]() )四邊形
)四邊形![]() 為矩形.
為矩形.
證:∵![]() 為
為![]() 中點,∴
中點,∴![]() .
.
又∵![]() ,∴四邊形
,∴四邊形![]() 為平行四邊形.
為平行四邊形.
又∵,∴
![]() .
.
在![]() 中.
中.
![]() .
.
∴![]() ,
,
∴四邊形![]() 為矩形.
為矩形.
“點睛”本題考查了二次函數綜合題,利用函數值相等得出(5,c)是解題關鍵,又利用了待定系數法求函數解析式;利用解方程組得出交點坐標,又利用了勾股定理;利用了平行四邊形的判定;對角線互相平分的四邊形是平行四邊形.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數學 來源: 題型:
【題目】已知如圖,矩形OABC的長OA=![]() , 寬OC=1,將△AOC沿AC翻折得△APC.
, 寬OC=1,將△AOC沿AC翻折得△APC.
(1)求∠PCB的度數;
(2)若P,A兩點在拋物線y=![]() x2+bx+c上,求b,c的值,并說明點C在此拋物線上;
x2+bx+c上,求b,c的值,并說明點C在此拋物線上;
(3)題(2)中的拋物線與矩形OABC邊CB相交于點D,與x軸相交于另外一點E,若點M是x軸上的點,N是y軸上的點,以點E、M、D、N為頂點的四邊形是平行四邊形,試求點M、N的坐標.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八年級一班與二班的同學在一次數學測驗中的成績統計情況如下表:
班級 | 參加人數 | 中位數 | 平均數 | 方差 |
一 | 49 | 84 | 80 | 186 |
二 | 49 | 85 | 80 | 161 |
某同學分析后得到如下結論:
①一班與二班學生平均成績相同;
②二班優生人數多于一班(優生線85分)
③一班學生的成績相對穩定。其中正確的是( )
A. ①② B. ①③ C. ①②③ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是由四個小正方形拼接成的L形圖案,按下列 要求畫出圖形。

(1)請你用兩種方法分別在L形圖案中添畫一個小正方形,使它成為軸對稱圖形;
(2)請你在L形圖案中添畫一個小正方形,使它成為中心對稱圖形。
(3)請你在L}形圖案中移動一個小正方形,使它成為既是中心對稱圖形,又是軸對稱圖形。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s,下面四個結論正確的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度數不變,始終等于60°;④當第![]() 秒或第
秒或第![]() 秒時,△PBQ為直角三角形.
秒時,△PBQ為直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(滿分8分)我市重慶路水果市場某水果店購進甲、乙兩種水果.已知1千克甲種水果的進價比1千克乙種水果的進價多4元,購進2千克甲種水果與1千克乙種水果共需20元.
(1)求甲種水果的進價為每千克多少元?
(2)經市場調查發現,甲種水果每天銷售量y(千克)與售價m(元/千克)之間滿足如圖所示的函數關系,求y與m之間的函數關系;
(3)在(2)的條件下,當甲種水果的售價定為多少元時,才能使每天銷售甲種水果的利潤最大?最大利潤是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com