
某工廠現有甲種原料360千克,乙種原料290千克,計劃利用這兩種原料生產A、B兩種產品共50件,已知生產一件A種產品需用甲種原料9千克,乙種原料3千克,可獲利潤700元;生產一件B種產品,需用甲種原料4千克、乙種原料10千克,可獲利潤1200元.
(1)要求安排A、B兩種產品的生產件數,有哪幾種方案?請你設計出來.
(2)生產A、B兩種產品獲總利潤是y(元),其中一種的生產件數是x,試寫出y與x之間的函數關系式,并利用函數的性質說明(1)中的哪種生產方案獲總利潤最大?最大利潤是多少?
|
(1) 設安排生產A種產品x件,則生產B種產品是(50-x)件,根據題意,有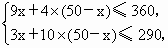
解這個不等式組得 30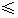 x x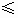 32. 32.
因為 x為整數,所以x只能取30、31、32,相應的可得50-x的值是20、19、18.所以,生產的方案有三種,即第一種生產方案:生產 A種產品30件,B種產品20件;第二種生產方案:生產A種產品31件,B種產品19件;第三種生產方案:生產A種產品32件,B種產品18件.(2) 設生產A種產品x件,則生產B種產品為(50-x)件,由題意,得y=700x+1200(50-x)=-500x+60000.(其中x只能取30,31,32)因為k=-500<0,所以此一次函數y隨x的增大而減小,所以,按第一種生產方案安排生產,獲總利潤最大,最大利潤是 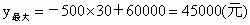 . . |


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:
| 需要甲原料 | 需要乙原料 | |
| 一種A種產品 | 7kg | 4kg |
| 一種B種產品 | 3kg | 10kg |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 需要用甲原料 | 需要用乙原料 | |
| 一件A種產品 | 7kg | 4kg |
| 一件B種產品 | 3kg | 10kg |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com