
【題目】如圖,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( )
,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( ) 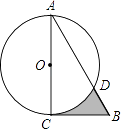
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
【答案】A
【解析】解:如圖連接OD、CD. ∵AC是直徑,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°﹣∠A=60°,
∵OC=OD,
∴△OCD是等邊三角形,
∵BC是切線.
∴∠ACB=90°,∵BC=2 ![]() ,
,
∴AB=4 ![]() ,AC=6,
,AC=6,
∴S陰=S△ABC﹣S△ACD﹣(S扇形OCD﹣S△OCD)
= ![]() ×6×2
×6×2 ![]() ﹣
﹣ ![]() ×3×3
×3×3 ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×32)
×32)
= ![]() ﹣
﹣ ![]() π.
π.
故選A.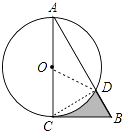
【考點精析】根據題目的已知條件,利用含30度角的直角三角形和扇形面積計算公式的相關知識可以得到問題的答案,需要掌握在直角三角形中,如果一個銳角等于30°,那么它所對的直角邊等于斜邊的一半;在圓上,由兩條半徑和一段弧圍成的圖形叫做扇形;扇形面積S=π(R2-r2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系內,已知直線l1經過原點O 及A(2,2 ![]() )兩點,將直線l1向右平移4個單位后得到直線l2 , 直線l2與x 軸交于點B.
)兩點,將直線l1向右平移4個單位后得到直線l2 , 直線l2與x 軸交于點B. 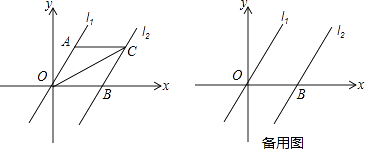
(1)求直線l2的函數表達式;
(2)作∠AOB 的平分線交直線l2于點C,連接AC.求證:四邊形OACB是菱形;
(3)設點P 是直線l2上一點,以P 為圓心,PB 為半徑作⊙P,當⊙P 與直線l1相切時,請求出圓心P 點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,角平分線AD、BE、CF相交于點H,過H點作HG⊥AC,垂足為G,那么∠AHE和∠CHG的大小關系為( )
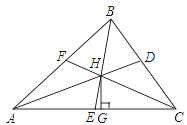
A. ∠AHE>∠CHG B. ∠AHE<∠CHG C. ∠AHE=∠CHG D. 不一定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解家長關注孩子成長方面的狀況,學校開展了針對學生家長的“您最關心孩子哪方面成長”的主題調查,調查設置了“健康安全”、“日常學習”、“習慣養成”、“情感品質”四個項目,并隨機抽取甲、乙兩班共100位學生家長進行調查,根據調查結果,繪制了如圖不完整的條形統計圖. 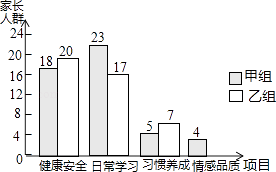
(1)補全條形統計圖.
(2)若全校共有3600位學生家長,據此估計,有多少位家長最關心孩子“情感品質”方面的成長?
(3)綜合以上主題調查結果,結合自身現狀,你更希望得到以上四個項目中哪方面的關注和指導?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在長方形ABCD中,AB=10cm,BC=8cm、點P從A出發,沿A、B、C、D路線運動,到D停止;點P的速度為每秒1cm,a秒時點P的速度變為每秒bcm,圖②是點P出發x秒后,△APD的面積S1(cm2)與x(秒)的函數關系圖象;
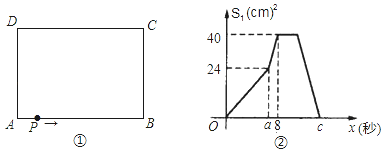
(1)根據圖②中提供的信息,求a、b及圖②中c的值;
(2)設點P離開點A的路程為y(cm),請寫出動點P改變速度后y與出發后的運動時間x(秒)的函數關系式;
(3)點P出發后幾秒,△APD的面積S1是長方形ABCD面積的![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,點A(-a,a)(a>0),點B(-a-4,a+3),C為該直角坐標系內的一點,連結AB,OC.若AB∥OC且AB=OC,則點C的坐標為________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各圖是在同一直角坐標系內,二次函數y=ax2+(a+c)x+c與一次函數y=ax+c的大致圖象,有且只有一個是正確的,正確的是( )
A.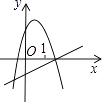
B.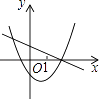
C.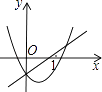
D.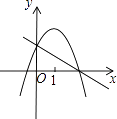
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有客房50間,當每間客房每天的定價為220元時,客房會全部住滿;當每間客房每天的定價增加10元時,就會有一間客房空閑,設每間客房每天的定價增加x元時,客房入住數為y間.
(1)求y與x的函數關系式(不要求寫出x的取值范圍);
(2)如果每間客房入住后每天的各種支出為40元,不考慮其他因素,則該賓館每間客房每天的定價為多少時利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣(2m+1)+( ![]() m2﹣1).
m2﹣1).
(1)求證:不論m取什么實數,該二次函數圖象與x軸總有兩個交點;
(2)若該二次函數圖象經過點(2m﹣2,﹣2m﹣1),求該二次函數的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com