用適當的方法解下列方程:
(1)5(x-3)2=3(x-3);
(2)y2+4y-3=0.
【答案】
分析:(1)將方程右邊的式子整體移項到左邊,提取公因式x-3將左邊化為積的形式,利用兩數相乘積為0,兩因式中至少有一個為0轉化為兩個一元一次方程,求出一次方程的解即可得到原方程的解;
(2)將方程常數項移項到右邊,方程左右兩邊都加上4,左邊化為完全平方式,右邊合并為一個常數,開方轉化為兩個一元一次方程,求出一次方程的解即可得到原方程的解.
解答:解:(1)5(x-3)
2=3(x-3),
移項得:5(x-3)
2-3(x-3)=0,
分解因式得:(x-3)[5(x-3)-3]=0,
可得x-3=0或5x-18=0,
解得:x
1=3,x
2=
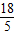
;
(2)y
2+4y-3=0,
移項得:y
2+4y=3,
配方得:y
2+4y+4=7,即(y+2)
2=7,
開方得:y+2=±
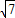
,
則y
1=-2+
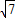
,y
2=-2-
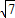
.
點評:此題考查了解一元二次方程-因式分解法及公式法,利用因式分解法解方程時,首先將方程右邊化為0,左邊化為積的形式,由利用兩數相乘積為0,兩因式中至少有一個為0轉化為兩個一元一次方程,求出一次方程的解即可得到原方程的解.

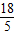 ;
;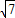 ,
,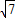 ,y2=-2-
,y2=-2-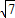 .
.

 名校課堂系列答案
名校課堂系列答案