
【題目】如圖,C是半圓O上一個動點,AB為半圓的直徑,D是弧BC的中點,過點D作半圓O的切線DE交AC的延長線于點E.
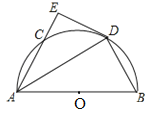
(1)求證:AE⊥DE;
(2)①已知CE=2,DE=4,則AB= ;
②連接OC,DC,當∠BAC= 度時,四邊形OBDC為菱形.
【答案】(1)見解析;(2)①10;②60.
【解析】
(1)連接OD,利用切線的性質和三角形內角和解答即可;
(2)①連接OC、CD、OD,并過點D作AB邊上的垂線,垂足為H,利用全等三角形的判定和性質以及勾股定理解答即可;
②利用菱形的性質解答即可.
(1)連接OD.
∵D是弧BC的中點,∴∠EAD=∠DAB.
∵OA=OD,∴∠DAB=∠ADO.
∵∠DAB+∠B=90°,∠ADO+∠ADE=90°,∴∠EDA=∠B,∴∠EAD+∠EDA=90°,∴∠AED=90°,∴AE⊥DE;
(2)①如圖,連接OC、CD、OD,并過點D作AB邊上的垂線,垂足為H.
∵∠AED=∠AHD=90°,∠EAD=∠DAH,AD=AD,∴△AED≌△AHD(AAS),∴DE=DH=4.
∵D是![]() 的中點,∴CD=BD.
的中點,∴CD=BD.
∵∠CED=∠BHD=90°,CD=BD,DE=DH,∴Rt△CED≌Rt△BHD(HL),∴CE=HB=2.
在Rt△OHD中,設OD=r,則OH=r﹣2,由勾股定理得:OD2﹣OH2=DH2,即r2﹣(r﹣2)2=42,解得:r=5,∴AB=2r=10;
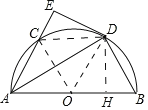
②連接OC,DC,當∠BAC=60度時,四邊形OBDC為菱形,理由如下:
∵∠BAC=60°,OA=OC,∴△ACO是等邊三角形,∴∠DAB=30°,∴∠B=60°,∴OB=OD=DB,∴OC=OB=BD=CD,∴四邊形OBDC是菱形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某文具店銷售甲、乙兩種圓規,當銷售5只甲種、1只乙種圓規,可獲利潤25元,銷售6只甲種、3只乙種圓規,可獲利潤39元.
(1)問該文具店銷售甲、乙兩種圓規,每只的利潤分別是多少元?
(2)在(1)中,文具店共銷售甲、乙兩種圓規50只,其中甲種圓規為a只,求文具店所獲得利潤P與a的函數關系式,并求當a≥30時P的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是線段
是線段![]() 上一點,
上一點,![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 的長為半徑作⊙
的長為半徑作⊙![]() ,過點
,過點![]() 作
作![]() 的垂線交⊙
的垂線交⊙![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() 在線段
在線段![]() 的延長線上,連接
的延長線上,連接![]() 交⊙
交⊙![]() 于點
于點![]() ,以
,以![]() ,
,![]() 為邊作
為邊作![]() .
.
(1)求證:![]() 是⊙
是⊙![]() 的切線;
的切線;
(2)若![]() ,求四邊形
,求四邊形![]() 與⊙
與⊙![]() 重疊部分的面積;
重疊部分的面積;
(3)若![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 和
和![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
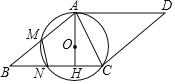
【題目】如圖,在菱形ABCD中,∠B=60°,AB=2,M為邊AB的中點,N為邊BC上一動點(不與點B重合),將△BMN沿直線MN折疊,使點B落在點E處,連接DE、CE,當△CDE為等腰三角形時,BN的長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
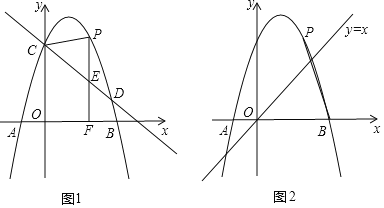
【題目】如圖1所示,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 經過點
經過點![]() ,與拋物線另一個交點為
,與拋物線另一個交點為![]() ,點
,點![]() 是拋物線上的一個動點,過
是拋物線上的一個動點,過![]() 點作
點作![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 于點
于點![]()
(1)求拋物線的解析式
(2)當點![]() 在直線
在直線![]() 上方,且
上方,且![]() 是以
是以![]() 為腰的等腰三角形時,求
為腰的等腰三角形時,求![]() 的坐標
的坐標
(3)如圖2所示,若點![]() 為對稱軸右側拋物線上一點,連接
為對稱軸右側拋物線上一點,連接![]() ,以
,以![]() 為直角頂點,線段
為直角頂點,線段![]() 為較長直角邊,構造兩直角邊比為
為較長直角邊,構造兩直角邊比為![]() 的
的![]() ,是否存在點
,是否存在點![]() ,使點
,使點![]() 恰好落在直線
恰好落在直線![]() 上?若存在,請直接寫出相應點
上?若存在,請直接寫出相應點![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸是![]() ,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
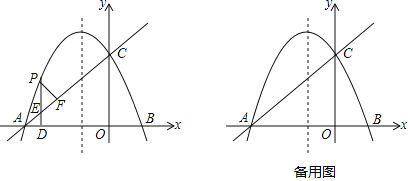
(1)求拋物線和直線l的解析式;
(2)點P是直線AC上方的拋物線上一個動點,過點P作PD⊥x軸于點D,交AC于點E,過點P作PF⊥AC,垂足為F,當△PEF≌△AED時,求出點P的坐標;
(3)在拋物線的對稱軸上是否存在點Q,使△ACQ為等腰三角形?若存在,直接寫出所有滿足條件的Q點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,∠ADC的平分線與AB交于E,點F在DE的延長線上,∠BFE=90°,連接AF、CF,CF與AB交于G.有以下結論:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
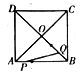
【題目】如圖,四邊形ABCD是正方形,![]() ,AC、BD交于點O,點P、Q分別是AB、BD上的動點,點P的運動路徑是
,AC、BD交于點O,點P、Q分別是AB、BD上的動點,點P的運動路徑是![]() ,點Q的運動路徑是BD,兩點的運動速度相同并且同時結束.若點P的行程為x,
,點Q的運動路徑是BD,兩點的運動速度相同并且同時結束.若點P的行程為x,![]() 的面積為y,則y關于x的函數圖象大致為( )
的面積為y,則y關于x的函數圖象大致為( )
A.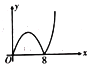 B.
B.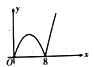 C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() ,以
,以![]() 為圓心,
為圓心,![]() 長為半徑作圓,
長為半徑作圓,![]() 經過點
經過點![]() ,與
,與![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() .
.

(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的半徑;
的半徑;
(3)在(2)的條件下,若![]() 的內切圓圓心為
的內切圓圓心為![]() ,直接寫出
,直接寫出![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com