
【題目】如圖,直線ll,l2交于點O,點P關于ll,l2的對稱點分別為P1、P2.
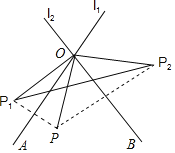
(1)若ll,l2相交所成的銳角∠AOB=60°,則∠P1OP2=______;
(2)若OP=3,P1P2=5,求△P1OP2的周長.
【答案】(1)120°;(2)△P1OP2的周長=11.
【解析】
(1)由于P關于l1、l2的對稱點分別為P1、P2,可得出∠P1AO=∠AOP,∠P2OB=∠POB,再根據∠AOB=60°即可求解;
(2)根據對稱的性質可知,OP1=OP=OP2=3,再根據P1P2=5即可求出△P1OP2的周長.
解:(1)∵P關于l1、l2的對稱點分別為P1、P2,
∴∠P1OA=∠AOP,∠P2OB=∠POB,
∴∠P1OP2=2(∠AOP+∠POB)=2∠AOB=2×60°=120°;
故答案為:120°;
(2)∵P關于l1、l2的對稱點分別為P1、P2,
∴OP1=OP=OP2=3,
∵P1P2=5,
∴△P1OP2的周長=OP1+OP2+P1P2=3+3+5=11.


科目:初中數學 來源: 題型:
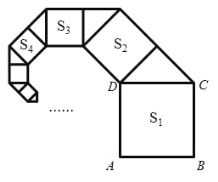
【題目】如圖,正方形 ABCD 的邊長為1,其面積為 S1,以CD 為斜邊作等腰直角三角形,以該等腰直角三角形的一條直角邊為邊向外作正方形,其面積記為 S2,…,按此規律繼續下去,則 S9的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題。
(1)如圖,在方格紙中先通過________,由圖形A得到圖形B,再由圖形B先________(怎樣平移),再________(怎樣旋轉)得到圖形C(對于平移變換要求回答出平移的方向和平移的距離;對于旋轉變換要求回答出旋轉中心、旋轉方向和旋轉角度);
(2)如圖,如果點P、P3的坐標分別為(0,0)、(2,1),寫出點P2的坐標是________;
(3)圖形B能繞某點Q順時針旋轉90°得到圖形C,則點Q的坐標是________;
(4)圖形A能繞某點R順時針旋轉90°得到圖形C,則點R的坐標是________; 注:方格紙中的小正方形的邊長為1個單位長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,A(1,0)、點B在y軸上,將三角形OAB沿x軸負方向平移,平移后的圖形為三角形DEC,且點C的坐標為(﹣3,2).
(1)直接寫出點E的坐標 ;
(2)在四邊形ABCD中,點P從點B出發,沿“BC→CD”移動.若點P的速度為每秒1個單位長度,運動時間為t秒,回答下列問題:
①當t= 秒時,點P的橫坐標與縱坐標互為相反數;
②求點P在運動過程中的坐標,(用含t的式子表示,寫出過程);
③當點P運動到CD上時,設∠CBP=x°,∠PAD=y°,∠BPA=z°,試問 x,y,z之間的數量關系能否確定?若能,請用含x,y的式子表示z,寫出過程;若不能,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點E在△ABC外部,點D在BC邊上,DE交AC于F,若∠1=∠2,∠C=∠E, AE=AC,
(1)求證: △ABC≌△ADE;
(2) 求證:∠2=∠3;
(3)當∠2=90°時,判斷△ABD的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
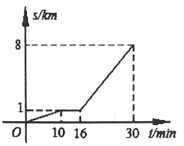
【題目】小亮從家步行到公交站臺,等公交車去學校.圖中折線表示小亮的行程![]() 與所花時間
與所花時間![]() 之間的函數關系.下列說法:
之間的函數關系.下列說法:![]() 他離家
他離家![]() 共用了
共用了![]() ;
;![]() 他等公交車的時間是
他等公交車的時間是![]() ;
;![]() 他步行的速度是
他步行的速度是![]() ;
;![]() 公交車的速度是
公交車的速度是![]() .正確的有________________(只填正確說法的序號).
.正確的有________________(只填正確說法的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:

(Ⅰ)圖1中a的值為 ;
(Ⅱ)求統計的這組初賽成績數據的平均數、眾數和中位數;
(Ⅲ)根據這組初賽成績,由高到低確定9人進入復賽,請直接寫出初賽成績為1.65m的運動員能否進入復賽.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com