
【題目】學校在八年級新生中舉行了全員參加的數學應用能力大賽,試卷題目共10題,每題10分.現分別從三個班中各隨機取10名同學的成績(單位:分),收集數據如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理數據:
人數 班級 | 60分人數 | 70分人數 | 80分人數 | 90分人數 | 100分人數 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均數 | 中位數 | 眾數 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析數據:
根據以上信息回答下列問題:
(1)請直接寫出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比較這三組樣本數據的平均數、中位數和眾數,你認為哪個班的成績比較好?請說明理由(寫兩條支持你結論的理由).
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() (2)2班的成績比較好.理由如下:通過對比,發現三個班平均分相同,但是2班的中位數要比1班和3班高,2班的眾數也要比1班和3班大,所以2班的成績比較好.
(2)2班的成績比較好.理由如下:通過對比,發現三個班平均分相同,但是2班的中位數要比1班和3班高,2班的眾數也要比1班和3班大,所以2班的成績比較好.
【解析】
(1)由收集到的數據可得a的值,利用3班的成績和平均數的公式即可計算平均數,根據2班的成績可得c和d的值;
(2)通過比較三個班的平均數,中位數和眾數,數值大的那個班的成績比較好即可得出答案.
(1)觀察可知2班成績為90分的有4人,故![]() ,
,
![]() ,
,
2班成績從小到大排序:60,70,80,80,80, 90,90,90,90,100,
所以中位數![]() ,
,
2班成績為90分的人數最多,所以眾數![]() ;
;
(2)2班的成績比較好.
理由如下:通過對比,發現三個班平均分相同,但是2班的中位數要比1班和3班高,2班的眾數也要比1班和3班大,所以2班的成績比較好.


科目:初中數學 來源: 題型:
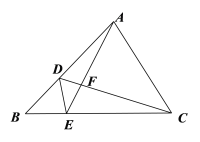
【題目】已知:如圖,在△ABC中,點D,E分別在邊AB,BC上,BABD=BCBE
(1)求證:△BDE∽△BCA;
(2)如果AE=AC,求證:AC2=ADAB.
查看答案和解析>>
科目:初中數學 來源: 題型:
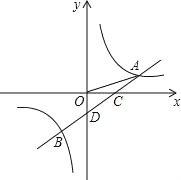
【題目】如圖,一次函數y=ax+b的圖象與反比例函數![]() 的圖象交于A,B兩點,與X軸交于點C,與Y軸交于點D,已知
的圖象交于A,B兩點,與X軸交于點C,與Y軸交于點D,已知![]() ,A(n,1),點B的坐標為(﹣2,m)
,A(n,1),點B的坐標為(﹣2,m)
(1)求反比例函數的解析式和一次函數的解析式;
(2)連結BO,求△AOB的面積;
(3)觀察圖象直接寫出一次函數的值大于反比例函數的值時x的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
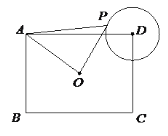
【題目】如圖,在矩形ABCD中,AB=3,BC=4,O為矩形ABCD的中心,以D為圓心1為半徑作⊙D,P為⊙D上的一個動點,連接AP、OP,則△AOP面積的最大值為( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
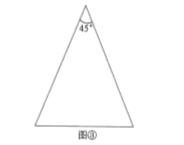
【題目】定義:如果兩條線段將一個三角形分成3個等腰三角形,我們把這兩條線段叫做這個三角形的三分線.
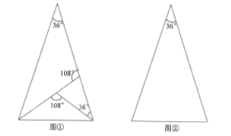
(1)圖①是頂角為![]() 的等腰三角形,這個三角形的三分線已經畫出,請你在圖②中用不同于圖①的方法畫出頂角為
的等腰三角形,這個三角形的三分線已經畫出,請你在圖②中用不同于圖①的方法畫出頂角為![]() 的等腰三角形的三分線,并標注每個等腰三角形頂角的度數(若兩種方法分得的三角形成3對全等三角形,則視為同一種);
的等腰三角形的三分線,并標注每個等腰三角形頂角的度數(若兩種方法分得的三角形成3對全等三角形,則視為同一種);
(2)圖③是頂角為![]() 的等腰三角形,請你在圖③中畫出頂角為
的等腰三角形,請你在圖③中畫出頂角為![]() 的等腰三角形的三分線,并標注每個等腰三角形頂角的度數.
的等腰三角形的三分線,并標注每個等腰三角形頂角的度數.
(3)![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的三分線,點
的三分線,點![]() 在
在![]() 邊上,點
邊上,點![]() 在
在![]() 邊上,且
邊上,且![]() ,
,![]() ,設
,設![]() ,則
,則![]() 所有可能的值為_________.
所有可能的值為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC是⊙O的直徑,點B,D在⊙O上,點E在⊙O外,∠EAB=∠D=30°.
(1)∠C的度數為 ;
(2)求證:AE是⊙O的切線;
(3)當AB=3時,求圖中陰影部分的面積(結果保留根號和π).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小微企業為加快產業轉型升級步伐,引進一批A,B兩種型號的機器.已知一臺A型機器比一臺B型機器每小時多加工2個零件,且一臺A型機器加工80個零件與一臺B型機器加工60個零件所用時間相等.
(1)每臺A,B兩種型號的機器每小時分別加工多少個零件?
(2)如果該企業計劃安排A,B兩種型號的機器共10臺一起加工一批該零件,為了如期完成任務,要求兩種機器每小時加工的零件不少于72件,同時為了保障機器的正常運轉,兩種機器每小時加工的零件不能超過76件,那么A,B兩種型號的機器可以各安排多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
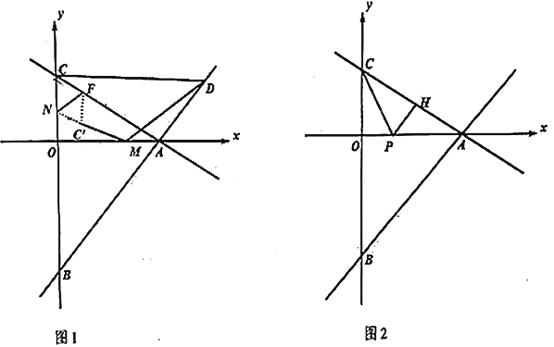
【題目】如圖1,已知直線![]() 和直線
和直線![]() 交于
交于![]() 軸上一點
軸上一點![]() ,且分別交
,且分別交![]() 軸于點
軸于點![]() 、點
、點![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)如圖1,點![]() 是直線
是直線![]() 上一點,且在
上一點,且在![]() 軸上方,當
軸上方,當![]() 時,在線段
時,在線段![]() 上取一點
上取一點![]() ,使得
,使得![]() ,點
,點![]() 分別為
分別為![]() 軸、
軸、![]() 軸上的動點,連接
軸上的動點,連接![]() ,將
,將![]() 沿
沿![]() 翻折至
翻折至![]() ,求
,求![]() 的最小值;
的最小值;
(3)如圖2,![]() 分別為射線
分別為射線![]() 上的動點,連接
上的動點,連接![]() 是否存在這樣的點
是否存在這樣的點![]() ,使得
,使得![]() 為等腰三角形,
為等腰三角形,![]() 為直角三角形同時成立.請直接寫出滿足條件的點
為直角三角形同時成立.請直接寫出滿足條件的點![]() 坐標.
坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com