
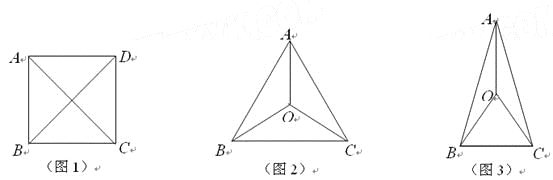
【題目】在平面上有且只有4個點,這4個點中有一個獨特的性質:連結每兩點可得到6條線段,這6條線段有且只有兩種長度.我們把這四個點稱作準等距點.例如正方形ABCD的四個頂點(如圖1),有AB=BC=CD=DA,AC=BD.其實滿足這樣性質的圖形有很多,如圖2中A、B、C、O四個點,滿足AB=BC=CA,OA=OB=OC;如圖3中A、B、C、O四個點,滿足OA=OB=OC=BC,AB=AC.
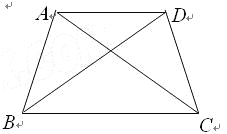
(1)如圖,若等腰梯形ABCD的四個頂點是準等距點,且AD∥BC.
①寫出相等的線段(不再添加字母);
②求∠BCD的度數.
(2)請再畫出一個四邊形,使它的四個頂點為準等距點,并寫出相等的線段.
【答案】(1)①AB=DC=AD, AC=BD=BC.②∠BCD=72°.(2)見解析.
【解析】
(1)①結合等腰梯形的性質及題意所表述的含義可寫出符合題意的結論.②先證△ABC≌△DCB,得出∠DBC=∠ACB,根據題意可求得∠BDC=∠BCD=2∠ACB,設∠ACB=x°,利用內角和定理可得出答案.
(2)可選擇畫菱形.
解:(1)①AB=DC=AD,AC=BD=BC,
②∵AC=BD,AB=DC,BC=BC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∵DC=AD,∠DAC=∠ACD,
∴∠ACD=∠ACB,
∵BC=BD,∠BDC=∠BCD=2∠ACB,
設∠ACB=x°,則∠BDC=∠BCD=2x°,∠DBC=x°,
∴2x+2x+x=180,
解得x=36,
∴∠BCD=72°.
(2)所畫圖形如下:四邊形ABCD是菱形(∠DAB=60°),
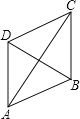
AB=BC=CD=AD=BD.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
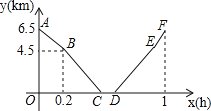
【題目】從甲地到乙地,先是一段上坡路,然后是一段平路,小明騎車從甲地出發,到達乙地后休息一段時間,然后原路返回甲地.假設小明騎車在上坡、平路、下坡時分別保持勻速前進,已知小明騎車上坡的速度比平路上的速度每小時少5km,下坡的速度比在平路上的速度每小時多5km,設小明出發xh后,到達離乙地ykm的地方,圖中的折線ABCDEF表示y與x之間的函數關系.
(1)小明騎車在平路上的速度為 km/h,他在乙地休息了 h.
(2)分別求線段AB、EF所對應的函數關系式.
(3)從甲地到乙地經過丙地,如果小明兩次經過丙地的時間間隔為0.85h,求丙地與甲地之間的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線l:y=![]() x+2與x軸交于點A,與y軸交于點B.已知點C(﹣2,0).
x+2與x軸交于點A,與y軸交于點B.已知點C(﹣2,0).
(1)求出點A,點B的坐標.
(2)P是直線AB上一動點,且△BOP和△COP的面積相等,求點P坐標.
(3)如圖2,平移直線l,分別交x軸,y軸于交于點A1,B1,過點C作平行于y軸的直線m,在直線m上是否存在點Q,使得△A1B1Q是等腰直角三角形?若存在,請直接寫出所有符合條件的點Q的坐標.
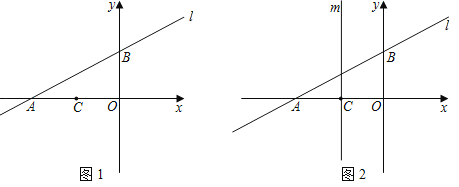
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=3x與反比例函數y=![]() 的圖象交于點A,B,點P在以C(﹣4,0)為圓心,1為半徑的⊙C上,Q是AP的中點,若OQ長的最大值為
的圖象交于點A,B,點P在以C(﹣4,0)為圓心,1為半徑的⊙C上,Q是AP的中點,若OQ長的最大值為![]() ,則k的值為_____.
,則k的值為_____.
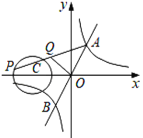
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 中函數y與自變量x之間部分對應值如下表所示,點
中函數y與自變量x之間部分對應值如下表所示,點![]()
![]() 在函數圖象上
在函數圖象上
x | … | 0 | 1 | 2 | 3 | … |
y | … | m | n | 3 | n | … |
則表格中的m=______;當![]() 時,
時,![]() 和
和![]() 的大小關系為______.
的大小關系為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在單位為1的方格紙上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜邊在x軸上,斜邊長分別為2,4,6,…的等直角三角形,若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,1),A3(0,0),則依圖中所示規律,A2019的坐標為( )
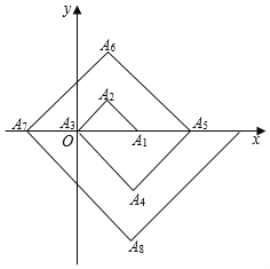
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,正方形OABC的頂點A、C分別在x,y軸上,且AO=1.將正方形OABC繞原點O順時針旋轉90°,且A1O=2AO,得到正方形OA1B1C1,再將正方OA1B1C1繞原點O順時針旋轉90°,且A2O=2A1O,得到正方形OA2B2C2…以此規律,得到正方形OA2019B2019C2019,則點B2019的坐標為_____.
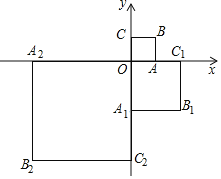
查看答案和解析>>
科目:初中數學 來源: 題型:
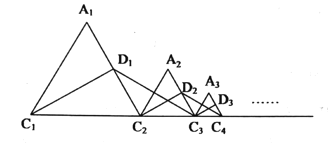
【題目】如圖,等邊![]() 的周長為1,作
的周長為1,作![]() 于
于![]() ,在
,在![]() 的延長線上取點
的延長線上取點![]() ,使
,使![]() ,連接
,連接![]() ,以
,以![]() 為邊作等邊
為邊作等邊![]() ;作
;作![]() 于
于![]() ,在
,在![]() 的延長線上取點
的延長線上取點![]() ,使
,使![]() ,連接
,連接![]() ,以
,以![]() 為邊作等邊
為邊作等邊![]() ;…且點
;…且點![]() ,
,![]() ,
,![]() ,…都在直線
,…都在直線![]() 同側,如此下去,可得到
同側,如此下去,可得到![]() 的邊長為__________.(
的邊長為__________.(![]() ,且
,且![]() 為整數)
為整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
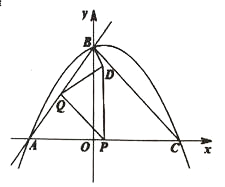
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過
經過![]() ,
,![]() 兩點,與
兩點,與![]() 軸正半軸交于點
軸正半軸交于點![]() ,連接
,連接![]() ,
,![]() 為線段
為線段![]() 上的動點,
上的動點,![]() 與
與![]() ,
,![]() 不重合,作
不重合,作![]() 交
交![]() 于
于![]() ,
,![]() 關于
關于![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)當點![]() 在拋物線上時,求點
在拋物線上時,求點![]() 的坐標;
的坐標;
(3)設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() .
.
①直接寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
②當![]() 為直角三角形時,直接寫出
為直角三角形時,直接寫出![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com