臺州高速三門段某處一交警10:05接到上司命令,要求他馬上到前方12km處攔截一沖卡的犯罪嫌疑人(最大速度勻速逃跑),此時警車速度指針為30千米/小時,里程表示數為4357千米,他馬上開足馬力,幾分鐘后速度指針為120千米/小時(最大車速,此后保持勻速),里程表示數為4362千米,若這段時間汽車的速度是勻速增加的,請問:
(1)警車勻加速用了幾分鐘?警車速度每分鐘增加多少千米/小時?
(2)里程表顯示4360km時,是幾點幾分?(精確到分)
(3)若要求他在半小時內追上嫌疑人,則嫌疑人的最大車速為多少?
【答案】
分析:(1)根據時間=路程:速度即可解答.在規定時間內,速度增加了90千米/小時,即可求出每分鐘增加多少千米/小時;
(2)假設再過x分鐘,里程表顯示4360km,即在平均速度前提下,走了3千米,列方程解答.
(3)若要求他在半小時內追上嫌疑人,即在30分鐘內,警車所走的路程應該等于嫌疑人所走的路程加上12,列方程即可解答.
解答:解:
(1)由題意(4362-4357)÷
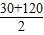
×60=4(分鐘),(120-30)÷4=22.5千米/小時.
(2)假設再過x分鐘,里程表顯示4360km.
則
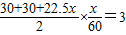
整理得:15x
2+40x-240=0
解之得:x
1≈3,x
2≈-6(舍去)
此時時間為10:08.
(3)設嫌疑人的最大車速為y千米/小時,則
5+
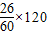
=

y+12
解之得:y=90
即嫌疑人的最大車速為90千米/小時.
點評:此題主要考查了平均速度的求法,以及方程的解法,難易程度適中.

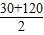 ×60=4(分鐘),(120-30)÷4=22.5千米/小時.
×60=4(分鐘),(120-30)÷4=22.5千米/小時.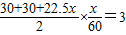
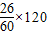 =
= y+12
y+12

 閱讀快車系列答案
閱讀快車系列答案