
 x+
x+ 與直線l2:y=-2x+16相交于點C,l1、l2分別交x軸于A、B兩點.矩形DEFG的頂點D、E分別在直線l1、l2上,頂點F、G都在x軸上,且點G與點B重合.
與直線l2:y=-2x+16相交于點C,l1、l2分別交x軸于A、B兩點.矩形DEFG的頂點D、E分別在直線l1、l2上,頂點F、G都在x軸上,且點G與點B重合.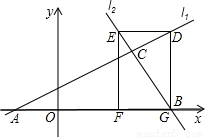
 x+
x+ =0,得x=-4.
=0,得x=-4.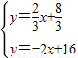 ,解得
,解得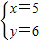
 AB•yC=
AB•yC= ×12×6=36.
×12×6=36. ×8+
×8+ =8,
=8,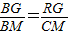 ,即
,即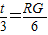 ,∴RG=2t,
,∴RG=2t, ×t×2t-
×t×2t- (8-t)×
(8-t)× (8-t),
(8-t),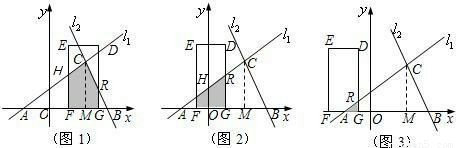
 t2+
t2+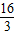 t+
t+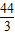 .
. (8-t),
(8-t), =
=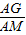 ,即
,即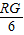 =
=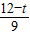 ,∴RG=
,∴RG= (12-t),
(12-t), (HF+RG)×FG=
(HF+RG)×FG= [
[ (8-t)+
(8-t)+ (12-t)]×4,
(12-t)]×4, t+
t+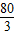 ;
; (12-t),
(12-t), AG•RG=
AG•RG= (12-t)×
(12-t)× (12-t)即S=
(12-t)即S= (12-t)2,
(12-t)2, t2-8t+48.
t2-8t+48.

科目:初中數學 來源: 題型:
 (2012•郯城縣一模)如圖,已知直線l1∥l2∥l3∥l4,相鄰兩條平行直線間的距離都是1,如果正方形ABCD的四個頂點分別在四條直線上,則cosα=( )
(2012•郯城縣一模)如圖,已知直線l1∥l2∥l3∥l4,相鄰兩條平行直線間的距離都是1,如果正方形ABCD的四個頂點分別在四條直線上,則cosα=( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖:已知直線l1∥l2,且l3、l4和l1、l2分別交于點A、B和點C、D,點P在AB上,設∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如圖:已知直線l1∥l2,且l3、l4和l1、l2分別交于點A、B和點C、D,點P在AB上,設∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.查看答案和解析>>
科目:初中數學 來源: 題型:
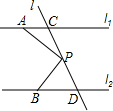 如圖,已知直線l1∥l2,直線l3和直線l1、l2交于點C和D,在直線l3上有點P(點P與點C、D不重合),點A在直線l1上,點B在直線l2上.
如圖,已知直線l1∥l2,直線l3和直線l1、l2交于點C和D,在直線l3上有點P(點P與點C、D不重合),點A在直線l1上,點B在直線l2上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com