
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于點A(﹣1,0),B(5,0)兩點,直線y=﹣ ![]() x+3與y軸交于點C,與x軸交于點D.點P是x軸上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E.設點P的橫坐標為m.
x+3與y軸交于點C,與x軸交于點D.點P是x軸上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E.設點P的橫坐標為m.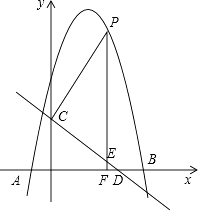
(1)求拋物線的解析式;
(2)若PE=5EF,求m的值;
(3)若點E′是點E關于直線PC的對稱點,是否存在點P,使點E′落在y軸上?若存在,請直接寫出相應的點P的坐標;若不存在,請說明理由.
【答案】
(1)
解:將點A、B坐標代入拋物線解析式,得:
![]() ,解得
,解得 ![]() ,
,
∴拋物線的解析式為:y=﹣x2+4x+5
(2)
解:∵點P的橫坐標為m,
∴P(m,﹣m2+4m+5),E(m,﹣ ![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP﹣yE|=|(﹣m2+4m+5)﹣(﹣ ![]() m+3)|=|﹣m2+
m+3)|=|﹣m2+ ![]() m+2|,
m+2|,
EF=|yE﹣yF|=|(﹣ ![]() m+3)﹣0|=|﹣
m+3)﹣0|=|﹣ ![]() m+3|.
m+3|.
由題意,PE=5EF,即:|﹣m2+ ![]() m+2|=5|﹣
m+2|=5|﹣ ![]() m+3|=|
m+3|=| ![]() m+15|
m+15|
①若﹣m2+ ![]() m+2=
m+2= ![]() m+15,整理得:2m2﹣17m+26=0,
m+15,整理得:2m2﹣17m+26=0,
解得:m=2或m= ![]() ;
;
②若﹣m2+ ![]() m+2=﹣(
m+2=﹣( ![]() m+15),整理得:m2﹣m﹣17=0,
m+15),整理得:m2﹣m﹣17=0,
解得:m= ![]() 或m=
或m= ![]() .
.
由題意,m的取值范圍為:﹣1<m<5,故m= ![]() 、m=
、m= ![]() 這兩個解均舍去.
這兩個解均舍去.
∴m=2或m= ![]()
(3)
解:假設存在.
作出示意圖如下:
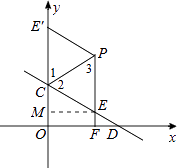
∵點E、E′關于直線PC對稱,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y軸,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四邊形PECE′是菱形.
當四邊形PECE′是菱形存在時,
由直線CD解析式y=﹣ ![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
過點E作EM∥x軸,交y軸于點M,易得△CEM∽△CDO,
∴ ![]() ,即
,即 ![]() ,解得CE=
,解得CE= ![]() |m|,
|m|,
∴PE=CE= ![]() |m|,又由(2)可知:PE=|﹣m2+
|m|,又由(2)可知:PE=|﹣m2+ ![]() m+2|
m+2|
∴|﹣m2+ ![]() m+2|=
m+2|= ![]() |m|.
|m|.
①若﹣m2+ ![]() m+2=
m+2= ![]() m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣
m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣ ![]() ;
;
②若﹣m2+ ![]() m+2=﹣
m+2=﹣ ![]() m,整理得:m2﹣6m﹣2=0,解得m1=3+
m,整理得:m2﹣6m﹣2=0,解得m1=3+ ![]() ,m2=3﹣
,m2=3﹣ ![]() .
.
由題意,m的取值范圍為:﹣1<m<5,故m=3+ ![]() 這個解舍去.
這個解舍去.
當四邊形PECE′是菱形這一條件不存在時,
此時P點橫坐標為0,E,C,E'三點重合與y軸上,也符合題意,
∴P(0,5)
綜上所述,存在滿足條件的點P,可求得點P坐標為(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
方法二:
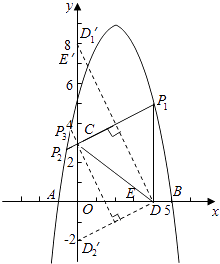
若E(不與C重合時)關于直線PC的對稱點E′在y軸上,則直線CD與直線CE′關于PC軸對稱.
∴點D關于直線PC的對稱點D′也在y軸上,
∴DD′⊥CP,∵y=﹣ ![]() x+3,
x+3,
∴D(4,0),CD=5,
∵OC=3,
∴OD′=8或OD′=2,
①當OD′=8時,D′(0,8),設P(t,﹣t2+4t+5),D(4,0),C(0,3),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() ,
,
∴2t2﹣7t﹣4=0,
∴t1=4,t2=﹣ ![]() ,
,
②當OD′=2時,D′(0,﹣2),
設P(t,﹣t2+4t+5),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() =﹣1,
=﹣1,
∴t1=3+ ![]() ,t2=3﹣
,t2=3﹣ ![]() ,
,
∵點P是x軸上方的拋物線上一動點,
∴﹣1<t<5,
∴點P的坐標為(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3).
﹣3).
若點E與C重合時,P(0,5)也符合題意.
綜上所述,存在滿足條件的點P,可求得點P坐標為(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
【解析】(1)利用待定系數法求出拋物線的解析式;(2)用含m的代數式分別表示出PE、EF,然后列方程求解;(3)解題關鍵是識別出當四邊形PECE′是菱形,然后根據PE=CE的條件,列出方程求解;當四邊形PECE′是菱形不存在時,P點y軸上,即可得到點P坐標.


科目:初中數學 來源: 題型:
【題目】如圖,小明在熱氣球A上看到正前方橫跨河流兩岸的大橋BC,并測得B,C兩點的俯角分別為60°和35°,已知大橋BC的長度為100m,且與地面在同一水平面上.求熱氣球離地面的高度. (結果保留整數,參考數據:sin35°≈ ![]() ,cos35°≈
,cos35°≈ ![]() ,tan35°≈
,tan35°≈ ![]() ,
, ![]() ≈1.7)
≈1.7)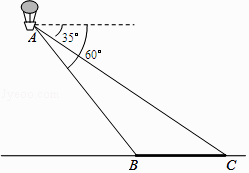
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB表示路燈,當身高為1.6米的小名站在離路燈1.6的D處時,他測得自己在路燈下的影長DE與身高CD相等,當小明繼續沿直線BD往前走到E點時,畫出此時小明的影子,并計算此時小明的影長. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F兩點在BC上,且四邊形AEFD是平行四邊形.
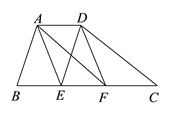
(1)AD與BC有何等量關系?請說明理由;
(2)當AB=DC時,求證:四邊形AEFD是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,∠BAC=90°,AD⊥BC于D,則下列結論中,正確的個數為( )
①AB⊥AC;②AD與AC互相垂直;③點C到AB的垂線段是線段AB;④點A到BC的距離是線段AD的長度;⑤線段AB的長度是點B到AC的距離;⑥線段AB是點B到AC的距離;

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
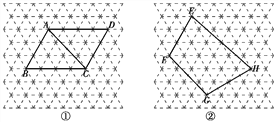
【題目】圖中的虛線網格是等邊三角形網格,它的每一個小三角形都是邊長為1的等邊三角形.
(1)邊長為1的等邊三角形的高=____;
(2)圖①中的ABCD的對角線AC的長=____;
(3)圖②中的四邊形EFGH的面積=____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現從A,B向甲、乙兩地運送蔬菜,A,B兩個蔬菜市場各有蔬菜14噸,其中甲地需要蔬菜15噸,乙地需要蔬菜13噸,從A到甲地運費50元/噸,到乙地30元/噸;從B地到甲運費60元/噸,到乙地45元/噸.
(1)設A地到甲地運送蔬菜x噸,請完成下表:
運往甲地(單位:噸) | 運往乙地(單位:噸) | |
A | x | |
B |
(2)設總運費為W元,請寫出W與x的函數關系式
(3)怎樣調運蔬菜才能使運費最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填寫推理理由
如圖,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.將∠E=∠1的過程填寫完整.
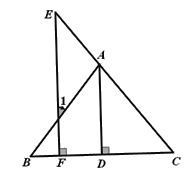
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意義 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D、E是BC邊上的點,連接AD,AE,以△ADE的邊AE所在直線為對稱軸作△ADE的軸對稱圖形△AD′E,連接D′C,若BD=CD′;
(1)求證:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com