
【題目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,在△ABC外作∠ACM= ![]() ∠ABC,點D為直線BC上的動點,過點D作直線CM的垂線,垂足為E,交直線AC于F.
∠ABC,點D為直線BC上的動點,過點D作直線CM的垂線,垂足為E,交直線AC于F.

(1)①當點D在線段BC上時,如圖1所示,求∠EDC的度數
②探究線段DF與EC的數量關系,并證明;
(2)當點D運動到CB延長線上時,請你畫出圖形,并證明此時DF與EC的數量關系.
【答案】(1)①22.5°;②DF=2CE,.理由見解析; (2)解:DF=2CE;理由見解析.
【解析】
(1)①由等腰直角三角形的性質得出∠ABC=∠ACB=45°,求出∠BCM=67.5°,即可得出∠EDC的度數;
②作∠PDE=22.5,交CE的延長線于P點,交CA的延長線于N,證明PD=CD,得出PC=2CE,由ASA證明△DNF≌△PNC,得出DF=PC,即可得出結論;
(2)作∠PDE=22.5,交CE的延長線于P點,交CA的延長線于N,證明PD=CD,得出PC=2CE,由ASA證明△DNF≌△PNC,得出DF=PC,即可得出結論.
(1)解:①如圖1所示:
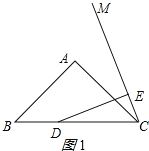
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM= ![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∵DE⊥CM,
∴∠EDC=90°-∠BCM=22.5°;
②DF=2CE.理由如下:
證明:作∠PDE=22.5°,交CE的延長線于P點,交CA的延長線于N,如圖2所示:
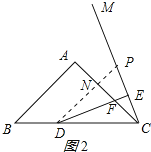
∵DE⊥PC,∠ECD=67.5°,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
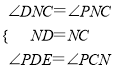 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE
(2)解:DF=2CE;理由如下:
證明:作∠PDE=22.5°,交CE的延長線于P點,交CA的延長線于N,如圖3所示:

∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
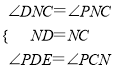 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.


科目:初中數學 來源: 題型:
【題目】某校為了開闊學生的視野,積極組織學生參加課外讀書活動,某讀書小組隨機抽取本校的部分學生,調查他們最喜愛的圖書類別(圖書分為文學類、文藝類、科普類、其他等四類),并將調查結果繪制成如圖所示的兩幅不完整的統計圖,請你結合圖中的信息解答下列問題
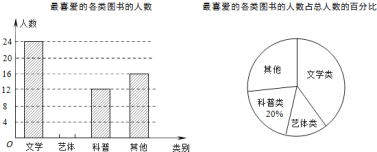
(1)被調查的學生人數為 人;
(2)科普類圓心角度數為 度,補全條形統計圖;
(3)已知該校有1800名學生,估計全校最喜愛文學類圖書的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=5,點E是邊CD的中點,將△ADE沿AE折疊后得到△AFE.延長AF交邊BC于點G,則CG為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AEM+∠CDN=180°,EC平分∠AEF.

(1)若∠EFC=62°,求∠C的度數;
(2)若CE⊥MN,垂足為點E,求證:∠FDE=∠FED.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀下列材料,并完成相應的任務:
在數學中,利用圖形在變化過程中的不變性質,常常可以找到解決問題的辦消去.著名美籍匈牙利數學家波利亞在他所著的《數學的發現》一書中有這樣一個例子:請問如何在一個三角形ABC的AC和BC兩邊上分別取一點X和Y,使得AX=BY=XY.(如圖)解決這個問題的操作步驟如下:
第一步,在CA上作出一點D,使得CD=CB,連接BD.第二步,在CB上取一點Y',作Y'Z∥CA,交BD于點Z',并在AB上取一點A',使Z'A'=Y'Z'.第三步,過點A作AZ∥A'Z',交BD于點Z.第四步,過點Z作ZY∥AC,交BC于點Y,再過點Y作YX∥ZA,交AC于點X.
則有AX=BY=XY.
下面是該結論的部分證明:
證明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴![]() .
.
同理可得![]() .∴
.∴![]() .
.
∵Z'A'=Y'Z',∴ZA=YZ.

在數學中,利用圖形在變化過程中的不變性質,常常可以找到解決問題的辦消去.著名美籍匈牙利數學家波利亞在他所著的《數學的發現》一書中有這樣一個例子:請問如何在一個三角形ABC的AC和BC兩邊上分別取一點X和Y,使得AX=BY=XY.(如圖)解決這個問題的操作步驟如下:
第一步,在CA上作出一點D,使得CD=CB,連接BD.第二步,在CB上取一點Y',作Y'Z∥CA,交BD于點Z',并在AB上取一點A',使Z'A'=Y'Z'.第三步,過點A作AZ∥A'Z',交BD于點Z.第四步,過點Z作ZY∥AC,交BC于點Y,再過點Y作YX∥ZA,交AC于點X.
則有AX=BY=XY.
下面是該結論的部分證明:
證明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴![]() .
.
同理可得![]() .∴
.∴![]() .
.
∵Z'A'=Y'Z',∴ZA=YZ.

任務:(1)請根據上面的操作步驟及部分證明過程,判斷四邊形AXYZ的形狀,并加以證明;
(2)請再仔細閱讀上面的操作步驟,在(1)的基礎上完成AX=BY=XY的證明過程;
(3)上述解決問題的過程中,通過作平行線把四邊形BA'Z'Y'放大得到四邊形BAZY,從而確定了點Z,Y的位置,這里運用了下面一種圖形的變化是 .
A.平移 B.旋轉 C.軸對稱 D.位似
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 與反比例函數
與反比例函數![]() 的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且
的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且![]() ⊥
⊥![]() .
.
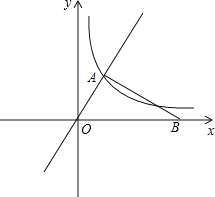
(1)求反比例函數的解析式;
(2)求點B的坐標;
(3)先在![]() 的內部求作點P,使點P到
的內部求作點P,使點P到![]() 的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知邊長為1的正方形ABCD中,P是對角線AC上的一個動點(與點A. C不重合),過點P作PE⊥PB,PE交射線DC于點E,過點E作EF⊥AC,垂足為點F,當點E落在線段CD上時(如圖),
(1)求證:PB=PE;
(2)在點P的運動過程中,PF的長度是否發生變化?若不變,試求出這個不變的值,若變化,試說明理由;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C、E分別在直線AB、DF上,小華想知道∠ACE和∠DEC是否互補,但是他沒有帶量角器,只帶了一副三角板,于是他想了這樣一個辦法:首先連結CF,再找出CF的中點O,然后連結EO并延長EO和直線AB相交于點B,經過測量,他發現EO=BO,因此他得出結論:∠ACE和∠DEC互補,而且他還發現BC=EF.小華的想法對嗎?為什么?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com