
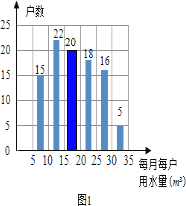
【題目】2014年1月,國家發改委出臺指導意見,要求2015年底前,所有城市原則上全面實行居民階梯水價制度.小明為了解市政府調整水價方案的社會反響,隨機訪問了自己居住小區的部分居民,就“每月每戶的用水量”和“調價對用水行為改變”兩個問題進行調查,并把調查結果整理繪制成下面的統計圖(圖1,圖2).

小明發現每月每戶的用水量在5m3-35m3之間,有8戶居民對用水價格調價漲幅抱無所謂,不會考慮用水方式的改變,根據小明繪制的圖表和發現的信息,完成下列問題:
(Ⅰ)n= ,小明調查了 戶居民,并補全圖2;
(Ⅱ)每月每戶用水量的中位數和眾數分別落在什么范圍?
(Ⅲ)如果小明所在小區有1800戶居民,請你估計“視調價漲幅采取相應的用水方式改變”的居民戶數有多少?
【答案】(1)n=210,96戶;(2)中位數落在15-20之間;眾數落在10-15之間;(3)1050戶.
【解析】
(1)首先根據圓周角等于360°,求出的值是多少即可;然后用“視水價格調價漲幅抱無所謂態度”的居民的戶數除以它占被調查的居民戶數的分率,求出小明調查了多少戶居民;最后求出每月每戶的用水量在15m3-20m3之間的居民的戶數,補全圖1即可.
(2)根據中位數和眾數的含義分別進行解答即可.
(3)根據分數乘法的意義,用小明所在小區居民的戶數乘以“視調價漲幅采取相應的用水方式改變”的居民戶數占被調查的居民戶數的分率,求出“視調價漲幅采取相應的用水方式改變”的居民戶數有多少即可.
解:(1)n=360-30-120=210,
∵8÷![]() =96(戶)
=96(戶)
∴小明調查了96戶居民.
每月每戶的用水量在15m3-20m3之間的居民的戶數是:
96-(15+22+18+16+5)
=96-76
=20(戶).
(2)96÷2=48(戶),15+12=37(戶),15+22+20=57(戶),
∵每月每戶的用水量在5m3-15m3之間的有37戶,每月每戶的用水量在5m3-20m3之間的有57戶,
∴把每月每戶用水量這組數據從小到大排列后,第48個、第49個數在15-20之間,
∴第48個、第49個數的平均數也在15-20之間,
∴每月每戶用水量的中位數落在15-20之間;
∵在這組數據中,10-15之間的數出現的次數最多,出現了22次,
∴每月每戶用水量的眾數落在10-15之間.
(3)∵1800×![]() =1050(戶),
=1050(戶),
視調價漲幅采取相應的用水方式改變”的居民戶數有1050戶.


科目:初中數學 來源: 題型:
【題目】依據下列解方程![]() 的過程,請在前面括號內填寫變形步驟,在后面的括號內填寫變形依據.
的過程,請在前面括號內填寫變形步驟,在后面的括號內填寫變形依據.
解:原方程可變形為![]() ,
,
去分母,得![]() .(____________________)
.(____________________)
去括號,得![]() .(____________________)
.(____________________)
移項,得![]() .(____________________)
.(____________________)
合并,得![]() .(合并同類項)
.(合并同類項)
(______),得![]() .(______________)
.(______________)
查看答案和解析>>
科目:初中數學 來源: 題型:
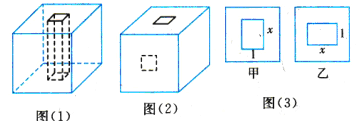
【題目】用橡皮泥做一個棱長為4cm的正方體.
(1)如圖(1),在頂面中心位置處從上到下打一個邊長為1cm的正方形通孔,打孔后的橡皮泥的表面積是多少?;
(2)如果在第(1)題打孔后,再在正面中心位置處(按圖(2)中的虛線)從前到后打一個邊長為1cm的正方形通孔,那么打孔后的橡皮泥的表面積為是多少?;
(3)如果把第(2)題中從前到后所打的正方形通孔擴大成一個長xcm、寬1cm的長方形通孔,能不能使所得橡皮泥的表面積為130cm2?如果能,請求出x;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,點A、B的坐標分別為(1,4)和(3,0),點C是y軸上的一個動點,且A、B、C三點不在同一條直線上,當△ABC的周長最小時,點C的坐標是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中數學 來源: 題型:
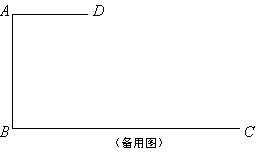
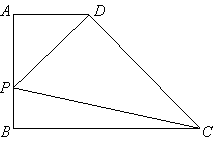
【題目】已知:如圖,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() .點
.點![]() 在線段
在線段![]() 上,聯結
上,聯結![]() ,過點
,過點![]() 作
作![]() 的垂線,與
的垂線,與![]() 相交于點
相交于點![]() .設線段
.設線段![]() 的長為
的長為![]() .
.
(1)當![]() 時,求線段
時,求線段![]() 的長;
的長;
(2)設△![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數解析式,并寫出函數的定義域;
的函數解析式,并寫出函數的定義域;
(3)當△![]() ∽△
∽△![]() 時,求線段
時,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出以下命題:
①函數![]() 是偶函數,但不是奇函數;
是偶函數,但不是奇函數;
②已知回歸直線方程為![]() ,樣本點的中心為
,樣本點的中心為![]() ,則
,則![]() ;
;
③函數![]() 圖象關于點
圖象關于點![]() 對稱且在
對稱且在![]() 上單調遞增;
上單調遞增;
④根據黨中央關于“精準”脫貧的要求,我州某農業經濟部門決定派出五位相關專家對三個貧困地區進行調研,每個地區至少派遣一位專家,其中甲、乙兩位專家需要派遣至同一地區,則不同的派遣方案種數有![]() 種;
種;
⑤已知雙曲線![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 的直線交雙曲線右支于
的直線交雙曲線右支于![]() 兩點,且
兩點,且![]() ,若
,若![]() ,則雙曲線的離心率為
,則雙曲線的離心率為![]() .
.
其中正確的命題序號為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系xOy中的位置如圖所示.

(1)作△ABC關于點C成中心對稱的△A1B1C1.
(2)將△A1B1C1向右平移4個單位,作出平移后的△A2B2C2.
(3)在x軸上求作一點P,使PA1+PC2的值最小,并寫出點P的坐標(不寫解答過程,直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,動點P從點B出發,沿BC,CD,DA運動到點A停止,設點P運動路程為x,△ABP的面積為y,如果y關于x的函數圖象如圖(2)所示,則矩形ABCD的面積是( )
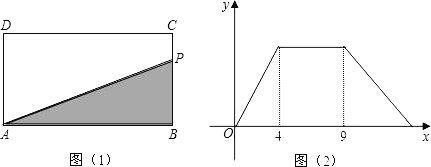
A. 10B. 16C. 20D. 36
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠為了檢驗甲、乙兩車間生產的同一種零件的直徑的合格情況,隨機各抽取了10個樣品進行檢測,已知零件的直徑均為整數,整理數據如下:(單位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲車間 | 1 | 3 | 4 | 2 |
乙車間 | 0 | 6 | 2 | 2 |
(1)分別計算甲、乙兩車間生產的零件直徑的平均數;
(2)直接說出甲、乙兩車間生產的零件直徑的中位數都在哪個小組內,眾數是否在其相應的小組內?
(3)若該零件的直徑在![]() 的范圍內為合格,甲、乙兩車間哪一個車間生產的零件直徑合格率高?
的范圍內為合格,甲、乙兩車間哪一個車間生產的零件直徑合格率高?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com