
【題目】(1)如圖1,在矩形ABCD中,點P為邊BC上一點,且![]() ,
, ![]() ,求BP的長;
,求BP的長;
(2)如圖2,在平行四邊形ABCD中, ![]() ,求
,求![]() 的長;
的長;

(3)如圖3,在四邊形ABCD中,AD∥BC, ![]() ,
, ![]() ,在BC邊上存在一點P,使得
,在BC邊上存在一點P,使得![]() ,則邊
,則邊![]() 的長滿足的條件為 。(請直接寫出結果)
的長滿足的條件為 。(請直接寫出結果)

【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)由四邊形ABCD是矩形,得到∠B=∠C=90°,根據余角的性質得到∠BAP=∠DPC,推出△ABP∽△PCD,根據相似三角形的性質即可得到結論;
(2)延長BC至點E,使得CD⊥DE,通過△ABP∽△DPE,列方程得到BP=1,過點P作PF⊥AB,解直角三角形即可得到結論;
(3)作AE⊥BC,DF⊥BC,得到∠AEP=∠DFP=90°,推出△AEP∽△PFD,根據相似三角形的性質得到AEDF=PEPF=4,由PE+PF≥2 ![]() ,即可得到結論.
,即可得到結論.
試題解析:(1)∵四邊形ABCD是矩形,
∴∠B=∠C=90°,
∵∠APD=∠B=90°,
∴∠PAB+∠APB=∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴![]() ,
,
設BP=x,∴![]()
∴x1=2,x2=8,又BP<PC,
∴BP=2;
(2)延長BC至點E,使得CD⊥DE,
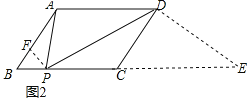
∵AB=2![]() ,BC=5,∠APD=∠B=45°,
,BC=5,∠APD=∠B=45°,
∴∠DPE=∠BAP,∠B=∠E=45°,
∴△ABP∽△DEP,
∴![]() ,
,
設BP=x,CE=![]() CD=4,
CD=4,
∴![]() ,
,
∴BP=1,
過點P作PF⊥AB,
則BF=PF=![]() ,AF=
,AF=![]() ,
,
∴AP=![]() ;
;
(3)AD≥4,
作AE⊥BC,DF⊥BC,
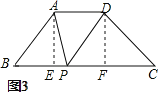
∴∠AEP=∠DFP=90°,
∵∠APD=90°,
∴∠EAP+∠APE=∠APE+∠DPF=90°,
∴∠EAP=∠DPF,
∴△AEP∽△PFD,
∴![]() ,
,
∴AEDF=PEPF=4,
∵PE+PF≥2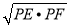 ,
,
∴AD=PE+PF≥4.
故答案為:AD≥4.


科目:初中數學 來源: 題型:
【題目】寧波軌道交通1號線、2號線建設總投資253.7億元,其中253.7億用科學記數法表示為( )
A.253.7×108
B.25.37×109
C.2.537×1010
D.2.537×1011
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于正比例函數y=2x的圖象,下列敘述錯誤的是( )
A. 點(﹣1,﹣2)在這個圖象上 B. 函數值y隨自變量x的增大而減小
C. 圖象關于原點對稱 D. 圖象經過一、三象限
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列代數式變形中,是因式分解的是( )
A.3ab(b﹣2)=3ab2﹣6ab
B.4x2﹣12x+3=4x(x﹣3)+3
C.3x﹣6y+6=3(x﹣2y)
D.﹣4x2+4x﹣1=﹣(2x﹣1)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大型企業為了保護環境,準備購買A、B兩種型號的污水處理設備共8臺,用于同時治理不同成分的污水,若購進A型2臺、B型3臺需54萬元,購買A型4臺、B型2臺需68萬元.
(1)求出A型、B型污水處理設備的單價;
(2)經核實,一臺A型設備一個月可處理污水220噸,一臺B型設備一個月可處理污水190噸,如果該企業每月的污水處理量不低于1 565噸,請你為該企業設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學小組的兩位同學準備測量兩幢教學樓之間的距離,如圖,兩幢教學樓AB和CD之間有一景觀池(AB⊥BD,CD⊥BD),一同學在A點測得池中噴泉處E點的俯角為42°,另一同學在C點測得E點的俯角為45°(點B,E,D在同一直線上),兩個同學已經在學校資料室查出樓高AB=15m,CD=20m,求兩幢教學樓之間的距離BD.
(結果精確到0.1m,參考數據:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com