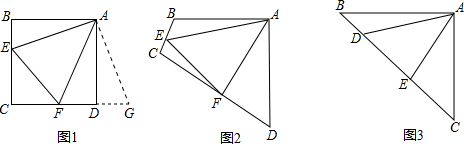
解:(1)在正△ABC中,AB=BC,∠ABC=∠ACB=60°
∴∠ABE=∠BCD=120°,
又∵BE=CD,
∴△ABE≌△BCD,
∴∠E=∠D
又∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°
由∠FBE=∠CBD,∠E=∠D得:△FBE∽△CBD
∴

,又BE=CD,
∴CD
2=BD•EF;
(2)由以上不難得:△AEB≌△BDC進一步證出,
△BEF∽△BDC,得出,∠AFB的度數等于∠DCB=90°,
同理可得:∠AFB度數為108°,(1)中式子成立;
故填:90°,108°,成立;
(3)由正三角形、正四邊形、正五邊形時,∠AFB的度數分別為60°,90°,108°,可得出“正n邊形”,其它條件不變,則∠AFB度數為

.
故填:

.
分析:(1)利用△ABE≌△BCD與△FBE∽△CBD得出

,從而得出原式正確;
(2)利用上面證明方法,可分別得出角度;
(3)由正三角形、正四邊形、正五邊形時,∠AFB的度數分別為60°,90°,108°,可得出“正n邊形”,其它條件不變,則∠AFB度數為

.
點評:此題主要考查了正三角邊形,正四邊形的性質,正五邊形的性質與等邊三角形與相似三角形的性質,題目綜合性很強.


 ,又BE=CD,
,又BE=CD, .
. .
. ,從而得出原式正確;
,從而得出原式正確; .
.