
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的半圓交AC于點D,交BC于點E,延長AE至點F,使EF=AE,連接FB、FC.
(1)求證:四邊形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圓的面積.
,BE=1,求半圓的面積.
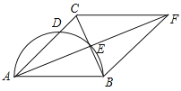
【答案】(1)見解析;(2)半圓的面積是![]()
【解析】
(1)由AB是直徑可得∠AEB=90°,根據等腰三角形的性質可得BE=CE,進而可得四邊形ABFC是平行四邊形,再根據菱形的定義即可證得結論;
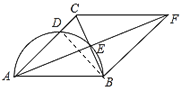
(2)連接![]() ,如圖,設
,如圖,設![]() ,根據勾股定理可得關于x的方程,解方程即可求出x,進一步即可求出半圓面積.
,根據勾股定理可得關于x的方程,解方程即可求出x,進一步即可求出半圓面積.
(1)證明:∵AB是直徑,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四邊形ABFC是平行四邊形,
∵AC=AB,
∴平行四邊形ABFC是菱形;
(2)解:連接![]() ,如圖,設
,如圖,設![]() ,則AC=x,
,則AC=x,
∵AB是直徑,∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
則![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
∴半圓的面積![]() .
.
答:半圓的面積是![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:
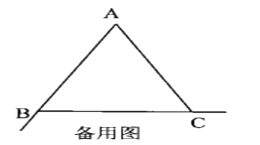
【題目】如圖, 已知等邊![]() , 點
, 點![]() 在射線
在射線![]() 上(不與
上(不與![]() 重合),連接
重合),連接![]() , 將射線
, 將射線![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 交射線
交射線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交直線
交直線![]() 于點
于點![]() .
.
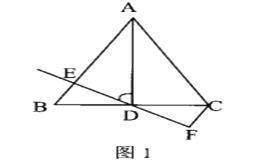
(1)如圖1,當點D為線段BC中點時,請直接寫出CF,BE,CD三條線段之間的數量;
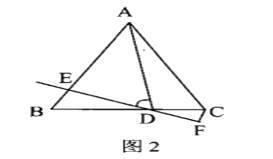
(2)如圖2,“點![]() 在線段
在線段![]() 上且不是
上且不是![]() 中點時,
中點時,![]() 中結論是否成立?若成立,請說明理由。若不成立,請寫出正確的結論并說明理由;
中結論是否成立?若成立,請說明理由。若不成立,請寫出正確的結論并說明理由;
(3)若![]() ,當
,當![]() 時,請直接寫出線段
時,請直接寫出線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,已知AB=2 ![]() ,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
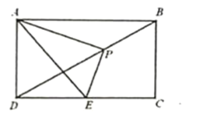
(1)求證:∠PAD=∠PEC;
(2)當點P是BD的中點時,求DE的值;
(3)在點P運動過程中,當DE= ![]() 時,求BP的值.
時,求BP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式規律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根據上面等式的規律:
(1)寫出第6個和第n個等式;
(2)證明你寫的第n個等式的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
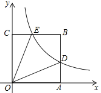
【題目】平面直角坐標系中,正方形OABC如圖放置,反比例函數![]() 的圖像交AB于點D,交BC于點E,已知A(
的圖像交AB于點D,交BC于點E,已知A(![]() ,0),∠DOE=30°,則k的值為( )
,0),∠DOE=30°,則k的值為( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
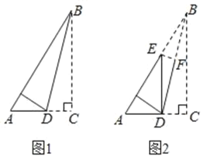
【題目】已知直角三角形紙片的兩直角邊AC與BC的比為3:4,首先將△ABC如圖1所示折疊,使點C落在AB上,折痕為BD,然后將△ABD如圖2所示折疊,使點B與點D重合,折痕為EF,則sin∠DEA的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年第七屆世界軍人運動會(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中國武漢舉行,這是中國第一次承辦綜合性國際軍事賽事,也是繼北京奧運會后,中國舉辦的規模最大的國際體育盛會.某射擊運動員在一次訓練中射擊了10次,成績如圖所示.下列結論中不正確的有( )個
①眾數是8;②中位數是8;③平均數是8;④方差是1.6.
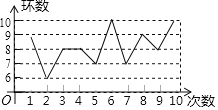
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
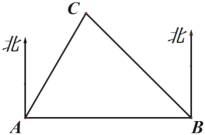
【題目】如圖,![]() 、
、![]() 是兩座現代化城市,
是兩座現代化城市,![]() 是一個古城遺址,
是一個古城遺址,![]() 城在
城在![]() 城的北偏東
城的北偏東![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正東方向,且
城的正東方向,且![]() 城與
城與![]() 城相距120千米,現在
城相距120千米,現在![]() 、
、![]() 兩城市修建一條筆直的高速公路.
兩城市修建一條筆直的高速公路.
(1)請你計算公路![]() 的長度(結果保留根號);
的長度(結果保留根號);
(2)若以![]() 為圓心,以60千米為半徑的圓形區域內為古跡和地下文物保護區,請你分析公路
為圓心,以60千米為半徑的圓形區域內為古跡和地下文物保護區,請你分析公路![]() 會不會穿越這個保護區,并說明理由.
會不會穿越這個保護區,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于A,B兩點,點B位于(4,0)、(5,0)之間,與y軸交于點C,對稱軸為直線x=2,直線y=﹣x+c與拋物線y=ax2+bx+c交于C,D兩點,D點在x軸上方且橫坐標小于5,則下列結論:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m為任意實數);④a<﹣1,其中正確的是( )

A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com