Question

在一個不透明的盒子里，裝有三個分別標有數字2，3，4的小球，它們的形狀、大小、質地等完全相同．小王先從盒子里隨機取出一個小球，記下數字為x；小張在剩下的二個小球中隨機取出一個小球，記下數字為y．
（1）用列表法或畫樹狀圖表示出（x，y）的所有可能出現的結果；
（2）計算由x，y確定的點（x，y）在函數y=-x+6圖象上的概率．

Answer 1

【答案】分析：（1）列出表格或畫出樹狀圖，然后即可得到所有的可能情況；
（2）根據一次函數圖象上點的坐標特征，把x的值代入直線解析式計算求出y的值，即可進行判斷，然后再根據概率公式進行計算即可得解．
解答：解：（1）列表如下：

x\y	2	3	4
2	--	（3，2）	（4，2）
3	（2，3）	--	（4，3）
4	（2，4）	（3，4）	--

畫樹狀圖如下：

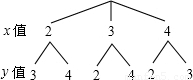
所以，所有可能出現的結果有：（2，3）、（2，4）、（3，2）、（3，4）、（4，2）、（4，3）；

（2）可能出現的結果共有6個，它們出現的可能性相等，
當x=2時，y=-2+6=4，
當x=3時，y=-3+6=3，
當x=4時，y=-4+6=2，
所以，滿足點（x，y）落在函數y=-x+6圖象上（記為事件A）的結果有2個，
即（2，4），（4，2）
所以P（A）=．
點評：本題考查了列表法或畫樹狀圖法，以及一次函數圖象上點的坐標特征，用到的知識點為：概率=所求情況數與總情況數之比．