
 ,求EF的長;
,求EF的長;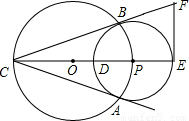
 (1)證明:連接PA、PB;
(1)證明:連接PA、PB;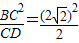 =4.
=4.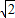 )2-16
)2-16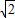 .
. PC,PB=PE;
PC,PB=PE; .
. 時,△PBD為等邊三角形.
時,△PBD為等邊三角形.

科目:初中數學 來源:2003年全國中考數學試題匯編《一元二次方程》(02)(解析版) 題型:選擇題
查看答案和解析>>
科目:初中數學 來源:2007年浙江省湖州二中提前招生考試數學試卷(解析版) 題型:選擇題
查看答案和解析>>
科目:初中數學 來源:2003年山東省青島市中考數學試卷(解析版) 題型:解答題
 ,求EF的長;
,求EF的長;
查看答案和解析>>
科目:初中數學 來源:2003年山東省青島市中考數學試卷(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com