
【題目】如圖1,在正方形![]() 中,
中,![]() 是對角線
是對角線![]() 上的一點,點
上的一點,點![]() 在
在![]() 的延長線上,
的延長線上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)連接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如圖2,若把正方形![]() 改為菱形
改為菱形![]() ,其他條件不變,當
,其他條件不變,當![]() 時,猜想
時,猜想![]() 與
與![]() 的數量關系,并證明你的猜想.
的數量關系,并證明你的猜想.
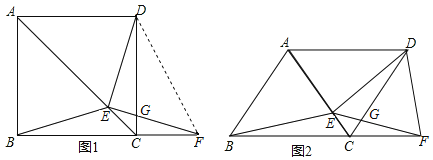
【答案】(1)證明見解析;(2)BE=![]() ;(3)BE=DF,理由見解析
;(3)BE=DF,理由見解析
【解析】
(1)根據正方形的性質證明△BCE≌△DCE即可;
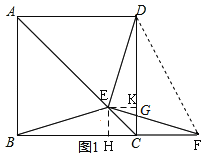
(2)過E作EK⊥DC于K,EH⊥BC于H,構建正方形EHCK,通過證明Rt△DEK≌Rt△FEH得出△DEF是等腰直角三角形,進而得解;
(3)先證明△BCE≌△DCE,得∠EBC=∠EDC,BE=ED,根據三角形內角和可得∠DEF=∠DCF=∠ABC=60°,進而得出△DEF是等邊三角形,可得結論.
(1)證明:∵四邊形ABCD是正方形,
∴BC=DC,∠BCE=∠DCE,
∵EC=EC,
∴△BCE≌△DCE,
∴BE=ED,
∵EF=ED,
∴EB=EF;
(2)解:如圖1,過E作EK⊥DC于K,EH⊥BC于H,
∴∠EKC=∠EHC=∠BCD=90°,
∴四邊形EHCK是矩形,
∵∠ECH=45°,
∴△EHC是等腰直角三角形,
∴EH=CH,
∴矩形EHCK是正方形,
∴EK=EH,
∴Rt△DEK≌Rt△FEH,
∴∠DEK=∠FEH,
∴∠DEK+∠FEK=∠FEH+∠FEK,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∵DF=2,
∴DE=![]() ,
,
∴BE=![]() ;
;
(3)解:BE=DF,理由是:
∵四邊形ABCD是菱形,
∴BC=DC,∠BCE=∠DCE,
∵EC=EC,
∴△BCE≌△DCE,
∴∠EBC=∠EDC,BE=ED,
∵EF=ED,
∴EB=EF,
∴∠EBC=∠EFC,
∴∠EDC=∠EFC,
∵∠EGD=∠CGF,
∴∠DEF=∠DCF=∠ABC=60°,
∴△DEF是等邊三角形,
∴DF=EF,
∴BE=DF.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖,過點P作PA,PB,分別與以OA為半徑的半圓切于A,B,延長AO交切線PB于點C,交半圓與于點D.
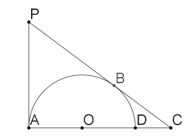
(1)若PC=5,AC=4,求BC的長;
(2)設DC:AD=1:2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李在學習了定理“直角三角形斜邊上的中線等于斜邊的一半”之后做了如下思考,請你幫他完成如下問題:
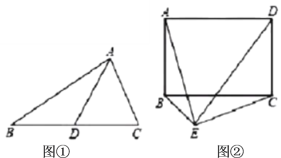
(1)他認為該定理有逆定理:“如果一個三角形某條邊上的中線等于該邊長的一半,那么這個三角形是直角三角形”應該成立.即如圖①,在![]() 中,
中,![]() 是
是![]() 邊上的中線,若
邊上的中線,若![]() ,求證:
,求證:![]() .
.
(2)如圖②,已知矩形![]() ,如果在矩形外存在一點
,如果在矩形外存在一點![]() ,使得
,使得![]() ,求證:
,求證:![]() .(可以直接用第(1)問的結論)
.(可以直接用第(1)問的結論)
(3)在第(2)問的條件下,如果![]() 恰好是等邊三角形,請求出此時矩形的兩條鄰邊
恰好是等邊三角形,請求出此時矩形的兩條鄰邊![]() 與
與![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
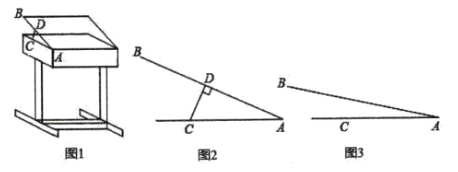
【題目】某課桌生產廠家研究發現,傾斜12°至24°的桌面有利于學生保持軀體自然姿勢.根據這一研究,廠家決定將水平桌面做成可調節角度得桌面.新桌面的設計圖如圖1,![]() 可繞點
可繞點![]() 旋轉,在點
旋轉,在點![]() 處安裝一根長度一定且
處安裝一根長度一定且![]() 處固定,可旋轉的支撐臂
處固定,可旋轉的支撐臂![]() ,
,![]() .
.
(1)如圖2,當![]() 時,
時,![]() ,求支撐臂
,求支撐臂![]() 的長;
的長;
(2)如圖3,當![]() 時,求
時,求![]() 的長.(結果保留根號)
的長.(結果保留根號)
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
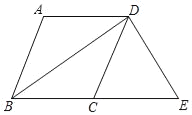
【題目】如圖,在四邊形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求證:四邊形ABCD是菱形;
(2)過點D作DE⊥BD,交BC的延長線于點E,若BC=5,BD=8,求四邊形ABED的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點A (2,4)和B(-4,m).
的圖象交于點A (2,4)和B(-4,m).
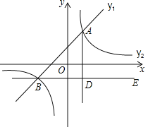
(1)求一次函數和反比例函數的表達式;
(2)請直接寫出y1>y2時,x的取值范圍;
(3)過點B作BE∥x軸,AD⊥BE于點D,點C是直線BE上一點,若AC=2CD,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】由甲、乙兩個工程隊承包某校校園綠化工程,甲、乙兩隊單獨完成這項工程所需時間比是3︰2,兩隊合做6天可以完成.
(1)求兩隊單獨完成此項工程各需多少天?
(2)此項工程由甲、乙兩隊合做6天完成任務后,學校付給他們20000元報酬,若
按各自完成的工程量分配這筆錢,問甲、乙兩隊各得到多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程![]() .
.
(1)求證:無論k取何實數值,方程總有實數根;
(2)若等腰△ABC的一邊長a=6,另兩邊長b、c恰好是這個方程的兩個根,求此三角形的三邊長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC中,AB=6,D是AC的中點,E是BC延長線上的一點,CE=CD,DF⊥BE,垂足為F.
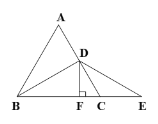
(1)求證:BF=EF;
(2)求△BDE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com