
【題目】在平面直角坐標系xOy中,點P和圖形W的“中點形”的定義如下:對于圖形W上的任意一點Q,連結PQ,取PQ的中點,由所以這些中點所組成的圖形,叫做點P和圖形W的“中點形”.
已知C(-2,2),D(1,2),E(1,0),F(-2,0).
(1)若點O和線段CD的“中點形”為圖形G,則在點![]() ,
,![]() ,
,![]() 中,在圖形G上的點是 ;
中,在圖形G上的點是 ;
(2)已知點A(2,0),請通過畫圖說明點A和四邊形CDEF的“中點形”是否為四邊形?若是,寫出四邊形各頂點的坐標,若不是,說明理由;
(3)點B為直線y=2x上一點,記點B和四邊形CDEF的中點形為圖形M,若圖形M與四邊形CDEF有公共點,直接寫出點B的橫坐標b的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)點A和四邊形CDEF的“中點形”是四邊形,各頂點的坐標為:(0,0)、(0,1)、(
;(2)點A和四邊形CDEF的“中點形”是四邊形,各頂點的坐標為:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.
【解析】
(1)依照題意畫出圖形,觀察圖形可知點O和線段CD的中間點所組成的圖形是線段C′D′,根據點A,C,D的坐標,利用中點坐標公式可求出點C′,D′的坐標,進而可得出結論;
(2)畫出圖形,觀察圖形可得出結論;
(3)利用一次函數圖象上點的坐標特征可得出點B的坐標為(n,2n),依照題意畫出圖形,觀察圖形可知:點B和四邊形CDEF的中間點只能在邊EF和DE上,當點B和四邊形CDEF的中間點在邊EF上時,利用四邊形CDEF的縱坐標的范圍,可得出關于n的一元一次不等式組,解之即可得出n的取值范圍;當點B和四邊形CDEF的中間點在邊DE上時,由四邊形CDEF的橫、縱坐標的范圍,可得出關于n的一元一次不等式組,解之即可得出n的取值范圍.綜上,此題得解.
解:(1)如圖:點O和線段CD的中間點所組成的圖形G是線段C′D′,
由題意可知:點C′為線段OC的中點,點D′為線段OD的中點.
∵點C的坐標為(-2,2),點D的坐標為(1,2),
∴點C′的坐標為(-1,1),點D′的坐標為(![]() ,1),
,1),
∴點O和線段CD的中間點所組成的圖形G即線段C′D′的縱坐標是1,橫坐標-1≤x≤![]() ,
,
∴點![]() ,
,![]() ,
,![]() 中,在圖形G上的點是
中,在圖形G上的點是![]() ,
,![]() ;
;
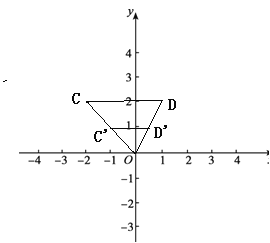
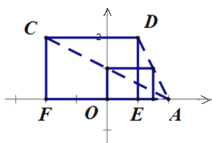
(2)點A和四邊形CDEF的“中點形”是四邊形.
各頂點的坐標為:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1).
,1).
(3)∵點B的橫坐標為b,
∴點B的坐標為(b,2b).
當點B和四邊形CDEF的中間點在邊EF上時,有![]() ,
,
解得:
當點B和四邊形CDEF的中間點在邊DE上時,有![]() ,
,
解得:1≤b≤2,
綜上所述:點B的橫坐標b的取值范圍為-1≤b≤0 或 1≤b≤2.
故答案為:(1)![]() ,
,![]() ;(2)點A和四邊形CDEF的“中點形”是四邊形,各頂點的坐標為:(0,0)、(0,1)、(
;(2)點A和四邊形CDEF的“中點形”是四邊形,各頂點的坐標為:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.


科目:初中數學 來源: 題型:
【題目】已知如圖:點(1,3)在函數y=![]() (x>0)的圖象上,矩形ABCD的邊BC在x軸上,E是對角線BD的中點,函數y=
(x>0)的圖象上,矩形ABCD的邊BC在x軸上,E是對角線BD的中點,函數y=![]() (x>0)的圖象又經過A、E兩點,點E的橫坐標為m,解答下列問題:
(x>0)的圖象又經過A、E兩點,點E的橫坐標為m,解答下列問題:
(1)求k的值;
(2)求點A的坐標;(用含m代數式表示)
(3)當∠ABD=45°時,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點都在格點上,點A的坐標為(2,2)請解答下列問題:
(1)畫出△ABC關于y軸對稱的△A1B1C1,并寫出A1的坐標.
(2)畫出△ABC繞點B逆時針旋轉90°后得到的△A2B2C2,并寫出A2的坐標.
(3)畫出△A2B2C2關于原點O成中心對稱的△A3B3C3,并寫出A3的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是邊AC上的一個動點,連接MB,過點M作MB的垂線交AB于點N. 設AM=x cm,AN=y cm.(當點M與點A或點C重合時,y的值為0)
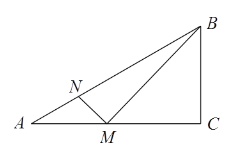
探究函數y隨自變量x的變化而變化的規律.
(1) 通過取點、畫圖、測量,得到了x與y的幾組對應值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:補全表格,相關數值保留一位小數)
(2)建立平面直角坐標系xOy,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:當AN=![]() AM時,AM的長度約為 cm(結果保留一位小數).
AM時,AM的長度約為 cm(結果保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國漢代數學家趙爽為了證明勾股定理,創制了一幅“弦圖”,后人稱其為“趙爽弦圖”(如圖(1)所示).圖(2)由弦圖變化得到,它是由八個全等的直角三角形拼接而成的記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3,若EF=4,則S1+S2+S3的值是( )
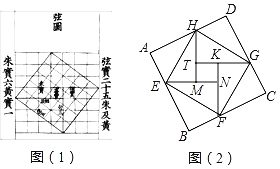
A.32B.38C.48D.80
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,點D,E分別在邊BC,AC上,DE∥AB,過點E作EF⊥DE,交BC的延長線于點F.
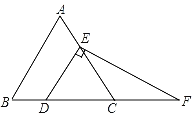
(1)求∠F的度數;
(2)若CD=4,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,B兩地被池塘隔開,小明通過下列方法測出了A,B間的距離:先在AB外選一點C,然后測出AC,BC的中點M,N,并測量出MN的長為12 m,由此他就知道了A,B間的距離,有關他這次探究活動的描述錯誤的是( )

A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】試題分析:根據三角形的中位線平行于第三邊并且等于第三邊的一半可得MN∥AB,MN=![]() AB,再根據相似三角形的判定解答.
AB,再根據相似三角形的判定解答.
試題解析:∵M、N分別是AC,BC的中點
∴MN∥AB,MN=![]() AB,
AB,
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中點
∴CM=MA
∴CM:MA=1:1
故描述錯誤的是D選項.
故選D.
考點:1.三角形中位線定理;2.相似三角形的應用.
【題型】單選題
【結束】
10
【題目】若關于![]() 的一元二次方程
的一元二次方程![]() +x-3m=0有兩個不相等的實數根,則
+x-3m=0有兩個不相等的實數根,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=x2+bx+c的對稱軸為直線x=1,拋物線與x軸交于A、B兩點(點A在點B的左側),且AB=4,又P是拋物線上位于第一象限的點,直線AP與y軸交于點D,與對稱軸交于點E,設點P的橫坐標為t.
(1)求點A的坐標和拋物線的表達式;
(2)當AE:EP=1:2時,求點E的坐標;
(3)記拋物線的頂點為M,與y軸的交點為C,當四邊形CDEM是等腰梯形時,求t的值.
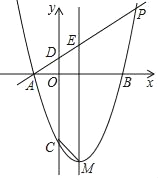
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com